10. 如图,一束平行光线照射三角尺ABC($∠ACB = 90^{\circ}$,$∠ABC = 30^{\circ}$),光线落在地面BD上,若$∠1 = 36^{\circ}$,则$∠2 = $
54
$^{\circ}$.
答案:
54
11. (12分)计算:
(1)$(-48)×(-\frac{1}{2} - \frac{5}{8} + \frac{7}{12})$; (2)$-1^{4} + 9÷(-3)^{2}×|-3 - 1|$.
(1)$(-48)×(-\frac{1}{2} - \frac{5}{8} + \frac{7}{12})$; (2)$-1^{4} + 9÷(-3)^{2}×|-3 - 1|$.
答案:
解:
(1)原式$=(-48)×(-\frac{1}{2})+(-48)×(-\frac{5}{8})+(-48)×\frac{7}{12}=24+30-28=26$.
(2)原式$=-1+9÷9×4=-1+4=3$.
(1)原式$=(-48)×(-\frac{1}{2})+(-48)×(-\frac{5}{8})+(-48)×\frac{7}{12}=24+30-28=26$.
(2)原式$=-1+9÷9×4=-1+4=3$.
12. (14分)如图,点E,F,H分别在直线CD,AB,AD上,EF交AD于点G,已知$∠A = ∠D$,$∠CEF + ∠B = 180^{\circ}$.
(1)EF与BH平行吗? 请说明理由;
(2)若$∠DGE = 110^{\circ}$,求$∠BHD$的度数.
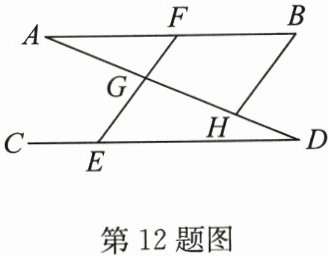
(1)EF与BH平行吗? 请说明理由;
(2)若$∠DGE = 110^{\circ}$,求$∠BHD$的度数.

答案:
解:
(1)$EF// BH$,理由如下:
因为$\angle A=\angle D$,所以$AB// CD$,
所以$\angle CEF+\angle AFE=180^{\circ}$.
因为$\angle CEF+\angle B=180^{\circ}$,
所以$\angle AFE=\angle B$,所以$EF// BH$.
(2)因为$\angle DGE=110^{\circ}$,
所以$\angle DGF=180^{\circ}-110^{\circ}=70^{\circ}$.
因为$EF// BH$,所以$\angle BHD=\angle DGF=70^{\circ}$.
(1)$EF// BH$,理由如下:
因为$\angle A=\angle D$,所以$AB// CD$,
所以$\angle CEF+\angle AFE=180^{\circ}$.
因为$\angle CEF+\angle B=180^{\circ}$,
所以$\angle AFE=\angle B$,所以$EF// BH$.
(2)因为$\angle DGE=110^{\circ}$,
所以$\angle DGF=180^{\circ}-110^{\circ}=70^{\circ}$.
因为$EF// BH$,所以$\angle BHD=\angle DGF=70^{\circ}$.
13. (14分)如图,数轴上三点M,O,N表示的数分别为-2,0,4,P为数轴上任意一点,其对应的数为x.
(1)如果点P到点M,N的距离相等,则$x = $
(2)数轴上是否存在点P,使点P到点M,N的距离之和是10? 若存在,求出x的值;若不存在,请说明理由.
(3)如果点P以每分钟1个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时点P到点M,N的距离相等,求t的值.
(1)如果点P到点M,N的距离相等,则$x = $
1
.(2)数轴上是否存在点P,使点P到点M,N的距离之和是10? 若存在,求出x的值;若不存在,请说明理由.
解:存在.当点P在点M的左侧时,$-2-x+4-x=10$,解得$x=-4$;
当点P在点M,N之间时,$x-(-2)+4-x=6$,不合题意;
当点P在点N的右侧时,$x-4+x-(-2)=10$,解得$x=6$.
所以数轴上存在点P,使点P到点M,N的距离之和是10,此时x的值为-4或6.
当点P在点M,N之间时,$x-(-2)+4-x=6$,不合题意;
当点P在点N的右侧时,$x-4+x-(-2)=10$,解得$x=6$.
所以数轴上存在点P,使点P到点M,N的距离之和是10,此时x的值为-4或6.
(3)如果点P以每分钟1个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时点P到点M,N的距离相等,求t的值.
解:当运动时间为t分钟时,点P对应的数为$-t$,
点M对应的数为$-2t-2$,点N对应的数为$-3t+4$.
当点P在点N左侧时,$-t-(-2t-2)=-3t+4-(-t)$,
解得$t=\frac{2}{3}$;
当点P在点N右侧时,$-2t-2=-3t+4$,解得$t=6$.
所以当点P到点M,N的距离相等时,t的值为$\frac{2}{3}$或6.
点M对应的数为$-2t-2$,点N对应的数为$-3t+4$.
当点P在点N左侧时,$-t-(-2t-2)=-3t+4-(-t)$,
解得$t=\frac{2}{3}$;
当点P在点N右侧时,$-2t-2=-3t+4$,解得$t=6$.
所以当点P到点M,N的距离相等时,t的值为$\frac{2}{3}$或6.
答案:
(1)1
(2)解:存在.当点P在点M的左侧时,$-2-x+4-x=10$,解得$x=-4$;
当点P在点M,N之间时,$x-(-2)+4-x=6$,不合题意;
当点P在点N的右侧时,$x-4+x-(-2)=10$,解得$x=6$.
所以数轴上存在点P,使点P到点M,N的距离之和是10,此时x的值为-4或6.
(3)解:当运动时间为t分钟时,点P对应的数为$-t$,
点M对应的数为$-2t-2$,点N对应的数为$-3t+4$.
当点P在点N左侧时,$-t-(-2t-2)=-3t+4-(-t)$,
解得$t=\frac{2}{3}$;
当点P在点N右侧时,$-2t-2=-3t+4$,解得$t=6$.
所以当点P到点M,N的距离相等时,t的值为$\frac{2}{3}$或6.
(1)1
(2)解:存在.当点P在点M的左侧时,$-2-x+4-x=10$,解得$x=-4$;
当点P在点M,N之间时,$x-(-2)+4-x=6$,不合题意;
当点P在点N的右侧时,$x-4+x-(-2)=10$,解得$x=6$.
所以数轴上存在点P,使点P到点M,N的距离之和是10,此时x的值为-4或6.
(3)解:当运动时间为t分钟时,点P对应的数为$-t$,
点M对应的数为$-2t-2$,点N对应的数为$-3t+4$.
当点P在点N左侧时,$-t-(-2t-2)=-3t+4-(-t)$,
解得$t=\frac{2}{3}$;
当点P在点N右侧时,$-2t-2=-3t+4$,解得$t=6$.
所以当点P到点M,N的距离相等时,t的值为$\frac{2}{3}$或6.
查看更多完整答案,请扫码查看


