《2025年启东中学作业本七年级数学上册苏科版徐州专版》

19. (8分)如图,B,C两点把线段AD分成三部分,且AB:BC:CD= 2:5:3,M为AD的中点.
(1)判断线段AB与CM的大小关系,并说明理由;
(2)若CM= 10,求AD的长.

答案： 1. （1）
设$AB = 2x$，因为$AB:BC:CD=2:5:3$，所以$BC = 5x$，$CD = 3x$。
则$AD=AB + BC+CD=2x + 5x+3x = 10x$。
因为$M$为$AD$的中点，所以$AM=\frac{1}{2}AD=\frac{1}{2}×10x = 5x$。
那么$CM=AM - AC$，又$AC = AB + BC=2x + 5x = 7x$（此处错误，应该是$CM = AC-AM$，$AC=AB + BC=2x + 5x=7x$），$AM = 5x$，所以$CM=AC - AM=7x-5x = 2x$。
因为$AB = 2x$，所以$AB = CM$。
2. （2）
已知$CM = 10$，由（1）知$CM = 2x$，所以$2x = 10$，解得$x = 5$。
又因为$AD = 10x$，把$x = 5$代入$AD = 10x$，得$AD=10×5 = 50$。
综上，（1）$AB = CM$；（2）$AD$的长为$50$。

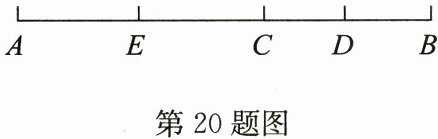
20. (8分)如图,AB= 10 cm,点E,C,D在线段AB上,且AC= 6 cm,E是线段AC的中点,D是线段BC的中点.求线段BD和DE的长.

答案： 1. 首先求$BC$的长度：
已知$AB = 10cm$，$AC = 6cm$，根据线段的和差关系$BC=AB - AC$。
所以$BC = 10−6=4cm$。
2. 然后求$BD$的长度：
因为$D$是线段$BC$的中点，根据中点的定义，若点$D$是线段$BC$中点，则$BD=\frac{1}{2}BC$。
把$BC = 4cm$代入可得$BD=\frac{1}{2}×4 = 2cm$。
3. 接着求$EC$的长度：
因为$E$是线段$AC$的中点，根据中点的定义，若点$E$是线段$AC$中点，则$EC=\frac{1}{2}AC$。
已知$AC = 6cm$，所以$EC=\frac{1}{2}×6 = 3cm$。
4. 最后求$DE$的长度：
根据线段的和差关系$DE=EC + CD$，又因为$CD = BD$（$D$是$BC$中点）。
所以$DE=EC + BD$。
把$EC = 3cm$，$BD = 2cm$代入可得$DE=3 + 2=5cm$。
综上，线段$BD$的长为$2cm$，线段$DE$的长为$5cm$。

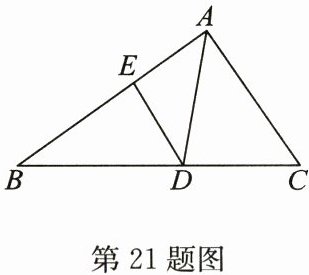
21. (10分)如图,在△ABC中,AD是角平分线,E为边AB上一点,连接DE,∠EAD= ∠EDA.试说明:DE//AC.

答案： 解:因为AD平分∠BAC，
所以∠BAD = ∠CAD.
因为∠EAD = ∠EDA，
所以∠CAD = ∠EDA，
所以DE // AC.

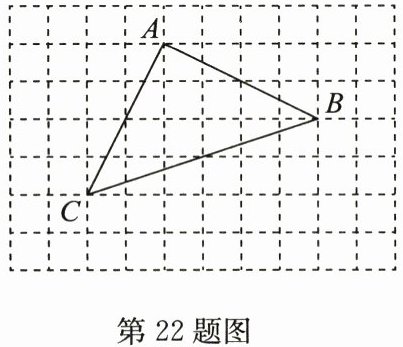
22. (10分)如图,方格纸中每个小正方形的边长均为1,△ABC的顶点均为格点.在方格纸中,按要求作图(不写作法):
(1)过点A作BC的垂线$l_1;$
(2)过点B作AC的平行线$l_2;$
(3)用尺规作∠ACP,使得∠ACP= ∠BCA(保留作图痕迹).

答案：
解:
(1)如答图所示，直线l₁即为所求.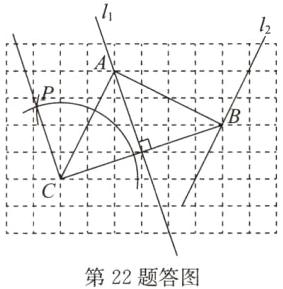
(2)如答图所示，直线l₂即为所求.
(3)如答图所示，∠ACP即为所求(答案不唯一).