《2025年综合应用创新题典中点六年级数学上册苏教版》

1. 选择。(每题5分,共10分)
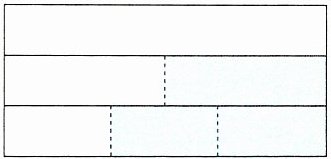
(1)新考法·数形结合 如图,将三个面积均为$\frac {1}{3}$平方厘米的相同的长方形拼在一起,组成一个大长方形,把第二个长方形平均分成2份,把第三个长方形平均分成3份,那么图中涂色部分的面积是多少平方厘米？下面列式正确的是(A)。

A.$\frac {1}{3}×\frac {1}{2}+\frac {1}{3}×\frac {2}{3}$
B.$\frac {1}{3}+\frac {2}{3}$
C.$\frac {1}{3}+\frac {1}{3}×\frac {2}{3}$
D.$\frac {2}{3}+\frac {1}{3}×\frac {2}{3}$
(2)新角度·逆向思考 在计算$\frac {5}{6}×(\frac {4}{5}+a)$时,没有考虑括号,计算结果比正确结果大$\frac {1}{2}$,则a的值是(D)。
A.$\frac {1}{2}$
B.$\frac {1}{3}$
C. 2
D. 3

答案： （1）A【点拨】第二个长方形中涂色部分的面积占第二个长方形面积的$\frac{1}{2}$，则第二个长方形中涂色部分的面积为$(\frac{1}{3}×\frac{1}{2})$平方厘米；第三个长方形中涂色部分的面积占第三个长方形面积的$\frac{2}{3}$，则第三个长方形中涂色部分的面积为$(\frac{1}{3}×\frac{2}{3})$平方厘米。
（2）D【点拨】根据乘法分配律可知$\frac{5}{6}×(\frac{4}{5}+a)=\frac{5}{6}×\frac{4}{5}+\frac{5}{6}a$，若不考虑括号，原式变成$\frac{5}{6}×\frac{4}{5}+a$，比$\frac{5}{6}×\frac{4}{5}+\frac{5}{6}a$大$a-\frac{5}{6}a=\frac{1}{6}a$，即$\frac{1}{6}a=\frac{1}{2}$，$a=3$。

2. 数学活动课上,聪聪和龙龙分别画出梯形和长方体,你能根据所给数据计算梯形的面积和长方体的表面积吗？(单位:厘米)(10分)

答案： $(\frac{5}{8}+\frac{12}{5})×\frac{20}{11}÷2=\frac{11}{4}$（平方厘米）
$(\frac{1}{2}×\frac{1}{3}+\frac{1}{2}×\frac{3}{7}+\frac{1}{3}×\frac{3}{7})×2=\frac{22}{21}$（平方厘米）
【点拨】梯形的面积=（上底+下底）×高÷2；长方体的表面积=（长×宽+长×高+宽×高）×2。

3. 能简算的要简算。(10分)
$\frac {99}{100}×101$
$(\frac {1}{2}+\frac {7}{12}-\frac {2}{9})÷\frac {1}{36}$

答案： $\frac{99}{100}×101$ $(\frac{1}{2}+\frac{7}{12}-\frac{2}{9})÷\frac{1}{36}$
$=\frac{99}{100}×(100+1)$ $=(\frac{1}{2}+\frac{7}{12}-\frac{2}{9})×36$
$=\frac{99}{100}×100+\frac{99}{100}$ $=\frac{1}{2}×36+\frac{7}{12}×36-\frac{2}{9}×36$
$=99+\frac{99}{100}$ $=18+21-8$
$=99\frac{99}{100}$ $=31$

4. 解决问题。(共30分)
(1)光明小学组织六年级同学到劳动基地参加劳动实践活动。六(1)班前$\frac {1}{3}小时共挖红薯\frac {3}{10}$千克,后2小时共挖红薯$\frac {48}{5}$千克,六(1)班平均每小时挖红薯多少千克？(10分)
(2)新情境·现代农业 张叔叔操控一台无人机为稻田喷洒农药,这天的工作记录如下:
上午:工作2小时,每小时喷洒$\frac {1}{5}$公顷
下午:工作2小时 一共喷洒$\frac {4}{7}$公顷
①按照上午、下午各自的工作效率,如果这台无人机上午、下午各工作4小时,一共可以喷洒多少公顷？(10分)
②如果张叔叔下午一共要给1公顷稻田喷洒农药,按照下午的工作效率,这台无人机还要工作多少小时？(10分)

答案： （1）$(\frac{3}{10}+\frac{48}{5})÷(\frac{1}{3}+2)=\frac{297}{70}$（千克）
答：六（1）班平均每小时挖红薯$\frac{297}{70}$千克。
【点拨】根据“工作总量÷工作时间=工作效率”列式解答，由题意可知工作总量是$(\frac{3}{10}+\frac{48}{5})$千克，工作时间是$(\frac{1}{3}+2)$小时。
（2）①$\frac{1}{5}×4+\frac{4}{7}×(4÷2)=\frac{68}{35}$（公顷）
答：一共可以喷洒$\frac{68}{35}$公顷。
②$(1-\frac{4}{7})÷(\frac{4}{7}÷2)=\frac{3}{2}$（小时）
答：这台无人机还要工作$\frac{3}{2}$小时。