第17页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. 用棱长为1的小正方体拼成如下图的大正方体后,把它们的表面分别涂上颜色,在第①、②、③个大正方体中,三面、两面、一面涂色以及没有涂色的小正方体各有多少个?
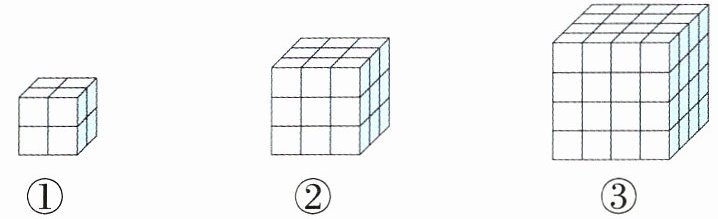
(1)按照这样的规律,第④、⑤、⑥、⑦、⑧个大正方体的结果会是怎样的呢?

(2)观察上表,若把一个表面涂色的棱长为$n(n≥3)$的大正方体切成棱长为1的小正方体,则:
①三面涂色的小正方体位于顶点上,每个顶点上有1个,共有
②两面涂色的小正方体位于棱上,每条棱上有
③一面涂色的小正方体位于面上,每个面上有
④没有涂色的小正方体位于大正方体内部,共有

8 8 8 0 12 24 0 6 24 0 1 8
(1)按照这样的规律,第④、⑤、⑥、⑦、⑧个大正方体的结果会是怎样的呢?

8 8 8 8 8 36 48 60 72 84 54 96 150 216 294 27 64 125 216 343
(2)观察上表,若把一个表面涂色的棱长为$n(n≥3)$的大正方体切成棱长为1的小正方体,则:
①三面涂色的小正方体位于顶点上,每个顶点上有1个,共有
8
个。②两面涂色的小正方体位于棱上,每条棱上有
n-2
个,共有12(n-2)
个。③一面涂色的小正方体位于面上,每个面上有
$(n-2)^2$
个,共有$6(n-2)^2$
个。④没有涂色的小正方体位于大正方体内部,共有
$(n-2)^3$
个。
答案:
1.(横排)8 8 8 0 12 24 0 6 24 0 1 8
(1)(横排)8 8 8 8 8 36 48 60 72 84 54 96 150 216 294 27 64 125 216 343(2)①8 ②n-2 12(n-2) $③(n-2)^2 6(n-2)^2 ④(n-2)^3$
(1)(横排)8 8 8 8 8 36 48 60 72 84 54 96 150 216 294 27 64 125 216 343(2)①8 ②n-2 12(n-2) $③(n-2)^2 6(n-2)^2 ④(n-2)^3$
2. 新情境·科普知识 激光切割技术采用激光束照射到钢板表面时释放的能量来使不锈钢熔化并蒸发。激光源一般用二氧化碳激光束。有一个表面涂色的大正方体,若用激光切割技术把它切割成若干个体积是1立方厘米的小正方体。已知一面涂色的小正方体有54个,则这个表面涂色的大正方体的体积是多少立方厘米?
答案:
2.54÷6=9(个) 9=3×3 3+2=5(厘米)5×5×5=125(立方厘米)答:这个表面涂色的大正方体的体积是125立方厘米。【点拨】一面涂色的小正方体有$6(n-2)^2$个,据此得出大正方体的棱长,再根据体积公式计算即可。
3. 如图是由三层小正方体摆成的物体。如果把它的外表面(包括底面,底面是正方形)全部涂成蓝色,再把它们分开,那么有多少个小正方体三面是蓝色的呢?


答案:
3.25-9-4=12(个) 4+12=16(个)答:有16个小正方体三面是蓝色的。【点拨】从上往下看:第一层有1个小正方体,露在外部5个面;第二层有3×3=9(个)小正方体,中间1个小正方体1个面也不露,其他8个小正方体中,四个顶点处的4个小正方体露出3个面,另外4个小正方体只露出2个面;第三层有5×5=25(个)小正方体,中间9个小正方体只露出1个面,四个顶点处的4个小正方体露出4个面,剩下的25-9-4=12(个)小正方体都露出3个面。有3个面露在外部的小正方体,即三面是蓝色的小正方体一共有4+12=16(个)。
4. 一个长方体木块,长6dm,宽5dm,高4dm,在它的表面涂上绿色,然后把它锯成棱长是1dm的小正方体木块。在锯成的小正方体木块中,三面涂绿色的有多少个?两面、一面涂绿色的各有多少个?六面都没有涂绿色的有多少个?
答案:
4.三面涂绿色:8个两面涂绿色:[(6-2)+(5-2)+(4-2)]×4=36(个)一面涂绿色:[(6-2)×(5-2)+(6-2)×(4-2)+(5-2)×(4-2)]×2=52(个)六面都没有涂绿色:(6-2)×(5-2)×(4-2)=24(个)答:三面涂绿色的有8个,两面、一面涂绿色的各有36个、52个,六面都没有涂绿色的有24个。
查看更多完整答案,请扫码查看


