《2025年综合应用创新题典中点六年级数学上册苏教版》

1. 将一块棱长是2dm的正方体铁块锻造成横截面是$50cm^2$的长方体铁条,锻造成的铁条长多少分米？(此题中的横截面是长方体的宽与高组成的面)

答案： 50cm²=0.5dm² 2×2×2÷0.5=16（dm）
答：锻造成的铁条长16dm。
【点拨】将正方体铁块锻造成长方体铁条后，体积不变。先求出正方体铁块的体积，再用正方体铁块的体积除以长方体铁条横截面的面积就是长方体铁条的长度。

2. 典典家有一个长方体玻璃鱼缸,从里面量,长7分米,宽4分米,深5分米。一天,典典不小心把鱼缸的一个面打碎了,为了保护金鱼,需要把鱼缸转过来盛水(如图所示)。算一算,用这个坏的鱼缸,最多能盛水多少升？

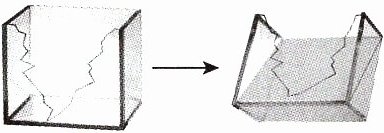
答案： 7×4×5÷2=70（立方分米）
70立方分米=70升
答：最多能盛水70升。
【点拨】由题图可知，这个坏的鱼缸内最多能盛水的体积是完整鱼缸的容积的一半。

3. 一个长方体,如果高增加5cm,就变成了一个正方体,这时表面积比原来增加了$180cm^2,$原来长方体的体积是多少立方厘米？

答案： 180÷4÷5=9（cm）
9×9×（9-5）=324（cm³）
答：原来长方体的体积是324cm³。
【点拨】根据题意，高增加5cm，就变成了一个正方体，说明原来长方体的长和宽相等，增加的表面积是四个完全相同的长方形的面积和，180÷4÷5=9（cm）就是原来长方体的长和宽，（9-5）cm就是原来长方体的高，最后结合长方体的体积公式求出原来长方体的体积。

4. 一个长方体,上、下两头各截下一个高4cm的小长方体后,正好得到一个正方体,且表面积比原来减少了$160cm^2。$原来长方体的体积是多少立方厘米？

答案： 160÷4÷（4+4）=5（cm）
5+4+4=13（cm）
5×5×13=325（cm³）
答：原来长方体的体积是325cm³。
【点拨】将截下的两个长方体合在一起看，相当于截下了一个高4+4=8（cm）的长方体后得到一个正方体，说明原来长方体的长和宽相等，表面积减少的部分相当于4个完全相同的长方形的面积和，据此求出原来长方体的正方形底面的边长为160÷4÷8=5（cm），原来长方体的高为5+8=13（cm），再根据长方体的体积公式计算即可。

5. 新情境·图表信息 数学课上同学们正在测量铁球的体积,步骤如下：

(1)取一个底面长20cm,宽15cm的长方体容器,注入部分水(如图①)。
(2)放入甲球,完全浸没在水中,水面上升4cm(如图②)。
(3)再放入乙球,这时有部分水溢出(如图③)。
(4)取出乙球,这时水面距离容器口6cm(如图④)。
甲球的体积是多少立方厘米？乙球的体积是多少立方厘米？

答案： 20×15×4=1200（cm³） 20×15×6=1800（cm³）
答：甲球的体积是1200cm³，乙球的体积是1800cm³。
【点拨】甲球完全浸没在水中后，甲球的体积=水面上升部分的体积，水面上升部分的体积等于长为20cm，宽为15cm，高为4cm的长方体的体积，根据长方体的体积公式，把数据代入即可求出甲球的体积。把乙球从水里拿出来后，乙球的体积=水面下降部分的体积，水面下降部分的体积等于长为20cm，宽为15cm，高为6cm的长方体的体积，根据长方体的体积公式，把数据代入即可求出乙球的体积。

6. 将棱长是1.5dm的正方体石块完全浸没在一个长方体水槽中,水面上升了0.75dm,然后又放入一个铁块并完全浸没,水面又上升了2dm(水没有溢出)。求铁块的体积。

答案： 1.5×1.5×1.5÷0.75×2=9（dm³）
答：铁块的体积是9dm³。
【点拨】放入正方体石块后，水面上升部分的体积就是正方体石块的体积，用正方体石块的体积除以水面上升的高度就是长方体水槽的底面积，用长方体水槽的底面积乘放入铁块后水面上升的高度即可求出铁块的体积。