《2025年5年中考3年模拟九年级物理全一册苏科版》

1.[2024 江苏无锡梅梁中学期末] 小海设计如图所示电路测量待测电阻$R_{x}$的阻值,$R_{0}$为阻值已知的定值电阻。步骤如下:①闭合 S、断开$S_{1}$,用电压表测出 $R_{0}$ (选填"$R_{0}$""$R_{x}$"或"电源")两端的电压$U_{1}$;②再闭合$S_{1}$,电压表示数为$U_{2}$;则闭合 S、断开$S_{1}$时,待测电阻$R_{x}$两端的电压为 $U_{2}-U_{1}$ ,阻值$R_{x}= $ $\frac{(U_{2}-U_{1})R_{0}}{U_{1}}$ 。(后两空均用$U_{1}$、$U_{2}和R_{0}$表示)

答案： $R_{0}$ $U_{2}-U_{1}$ $\frac{(U_{2}-U_{1})R_{0}}{U_{1}}$

2.[2024 陕西西安汇知中学期末] 有一个电压约为2V的电源(电压保持不变)、一个电流表(量程0~0.6A)、一个电压表(量程0~3V)、一个电阻箱(电路符号 ),开关和导线若干。请你合理选择器材设计实验,测出约为600Ω的未知定值电阻$R_{x}$的阻值。要求:
(1)画出实验电路图;
(2)写出主要实验步骤和需要测量的物理量;
(3)写出待测电阻$R_{x}$的表达式(用已知量和测量量表示)。

答案：

(1)如图所示　
(2)见解析
(3)$R_{x}=\frac{U_{1}R_{0}}{U_{2}-U_{1}}$

解析　
(1)电源电压约2V，未知定值电阻$R_{x}$阻值约为600Ω，由欧姆定律知，无论如何设计电路，通过定值电阻$R_{x}$的电流远远小于电流表的分度值0.02A，故用提供的电流表无法测出定值电阻$R_{x}$的阻值；可利用伏阻法测量，电路设计如答案图所示。
(2)①断开开关，电阻箱调到阻值最大处，按图连接实物图；②闭合开关，将电阻箱调到适当的位置，接入电路的电阻为$R_{0}$，读出电压表的示数为$U_{1}$；③将电阻箱调到0位置，读出电压表的示数为$U_{2}$。
(3)由
(2)可知，电源电压为$U_{2}$，当电阻箱接入电路的阻值为$R_{0}$时，电阻箱两端的电压$U_{0}=U_{2}-U_{1}$，电路中的电流$I_{0}=\frac{U_{0}}{R_{0}}=\frac{U_{2}-U_{1}}{R_{0}}$，未知电阻$R_{x}$的表达式是$R_{x}=\frac{U_{1}}{I_{0}}=\frac{U_{1}R_{0}}{U_{2}-U_{1}}$。

3.[新中考] 同学们在实验过程中,发现电压表不能正常使用,于是撤去电压表,又设计了以下4种方案($R_{L}$为阻值已知的定值电阻,电源电压恒定)。其中不能测出$R_{x}$的方案是A。如果 S、$S_{1}$都闭合时,电流表示数为$I_{1}$,闭合 S、断开$S_{1}$时,电流表示数为$I_{2}$,则电阻的表达式$R_{x}= \frac {R_{L}(I_{1}-I_{2})}{I_{2}}$为方案B的测量结果。

答案： A　B

4.[2024 江苏南京金陵汇文学校月考] 伏安法测电阻实验中电压表已损坏,电流表完好,设计了如图所示的电路,也完成了实验,请将下列实验步骤填写完整(滑动变阻器最大阻值为$R_{0}$):
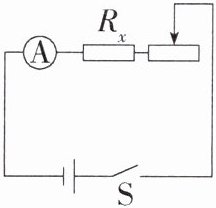
①闭合开关 S,调节滑动变阻器的滑片,当滑片位于最左端时,读出此时电流表的示数,记为$I_{1};$
②将滑片移到最右端,读出此时电流表的示数,记为$I_{2};$
③未知电阻$R_{x}=$$\frac{I_{2}R_{0}}{I_{1}-I_{2}}$(用已知量和测量量表示)。

答案： ②将滑片移到最右端 ③$\frac{I_{2}R_{0}}{I_{1}-I_{2}}$

5.[新中考] 小乐想用电源、一个电流表、两个开关和阻值已知的电阻$R_{0}测量未知电阻R_{x}$的阻值,连接了如图甲所示电路进行实验。当只闭合开关$S_{1}时电流表的示数为I_{1}$;闭合开关$S_{1}和S_{2}时电流表的示数为I_{2}$,则电阻$R_{x}= $$\frac{I_{1}R_{0}}{I_{2}-I_{1}}$(用$I_{1}$、$I_{2}和R_{0}$表示)。小明认为此电路不妥,理由是:缺少滑动变阻器，不能多次测量求平均值，减小误差;于是他设计了另外一种电路,如图乙所示,他认为只闭合开关$S_{1}$,调节滑动变阻器的滑片 P,测得$R_{0}$中的电流,保持滑片 P 位置不变,只闭合开关$S_{2}$,测得$R_{x}$中的电流,这样就可以测量电阻$R_{x}$的阻值。但是小乐认为也不妥,理由是两次实验中有一次电流表的正、负接线柱接反;于是他们在此基础上又设计了图丙的电路,他首先将开关 S 接到触点 1,移动滑动变阻器滑片 P,读出电流表示数为$I_{1}$,保持滑片 P 位置不变,然后将开关 S 接到触点 2,读出电流表示数$I_{2}$,则电阻$R_{x}= $$\frac{I_{2}R_{0}}{I_{1}-I_{2}}$(用$I_{1}$、$I_{2}和R_{0}$表示)。

答案： $\frac{I_{1}R_{0}}{I_{2}-I_{1}}$ 缺少滑动变阻器，不能多次测量求平均值，减小误差 两次实验中有一次电流表的正、负接线柱接反 $\frac{I_{2}R_{0}}{I_{1}-I_{2}}$