《2025年5年中考3年模拟九年级物理全一册苏科版》

8.[2024江苏常州武进一模]如图甲所示,长1 m的粗细均匀的光滑金属杆可绕O点转动,杆上有一光滑滑环,用竖直向上的测力计拉着滑环缓慢向右移动,使杆保持水平状态,测力计示数F与滑环离开O点的距离s的关系如图乙所示,则金属杆的重力为100N,滑环的重力为50N。

答案： 100 50 解析　由题意可知,金属杆是粗细均匀的一个杠杆,重心在金属杆的中点,当s = OA = 1m时,动力臂是阻力臂的二倍;由图乙可知,此时的动力F = 100N,根据$F_{1}L_{1}=F_{2}L_{2}$可知:$(F - G_{滑})L_{1}=GL_{2}$,即100N - $G_{滑}=\frac{1}{2}G$①;由图乙可知,当s = 0.1m时,$F' = 550$N,$L_{1}' = 0.1$m,$L_{2}= 0.5$m,根据$F_{1}L_{1}=F_{2}L_{2}$可知:$(F' - G_{滑})L_{1}'=GL_{2}$,即550N - $G_{滑}=5G$②;联立①②可得,$G_{滑}=50$N,G = 100N。

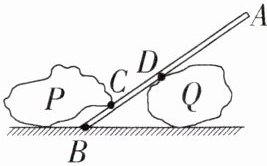
9.[2024江苏无锡惠山期中]如图所示,用一根自重可忽略不计的撬棒撬石块,若撬棒C点受到石块P垂直于撬棒向下的压力是2000 N,且AB= 2 m,BD= 0.6 m,CD= 0.4 m,则要撬动石块P所用的最小的力应为 ( )


A.600 N
B.400 N
C.150 N
D.200 N

答案：
D　①若以D点为支点,则作用在A点的最小力应垂直杠杆斜向下,此时AD为动力臂，CD为阻力臂，如图甲;②若以B点为支点,则作用在A点的最小力应垂直杠杆斜向上,此时AB为动力臂，BC为阻力臂，如图乙。由题意可知,AD ＜ AB,CD ＞ BC,所以②更省力;如图乙,以B为支点,动力臂$L_{AB}=2$m,阻力臂$L_{BC}=BD - CD = 0.6$m - 0.4m = 0.2m,由杠杆的平衡条件知,$F_{1}'×L_{AB}=F_{2}×L_{BC}$,$F_{1}'×2$m = 2000N×0.2m,解得$F_{1}' = 200$N。

10.[2025江苏苏州高新一中月考]如图所示,杠杆AB放在钢制圆柱体的正中央水平凹槽CD中,杠杆AB能以凹槽两端的C点或D点为支点在竖直平面内转动,长度AC= CD= DB= 0.5 m,杠杆左端有一个重物。当在B端通过细绳施加竖直向下的拉力F时,杠杆AB保持水平位置平衡。(杠杆、细绳的质量及摩擦忽略不计)

(1)若重物重力为6 N,能保持杠杆水平平衡的最小力F小=3N;
(2)若力F在某一范围内变化,仍能使得杠杆保持水平平衡,且这个范围内力F的最大变化量ΔF= 18 N,重物的重力G=12N。

答案： （1）3N （2）12N 解析　（1）由题意可知,重物的重力$G_{1}=6$N,AB = AC + CD + DB = 0.5m + 0.5m + 0.5m = 1.5m,杠杆水平平衡时有:$G_{1}×L_{G}=F×L_{F}$,即$F=\frac{L_{G}}{L_{F}}×G_{1}=\frac{L_{G}}{AB - L_{G}}×G_{1}$,当$L_{G}=AC$时,拉力最小,则$F_{小}=\frac{AC}{AB - AC}×G_{1}=\frac{0.5m}{1.5m - 0.5m}×6$N = 3N;（2）杠杆保持水平平衡,当以C点为支点时拉力最小,以D点为支点时拉力最大,由杠杆的平衡条件可得:$F_{小}'×CB = G×AC$,$F_{大}×DB = G×AD$,因CB = CD + DB = 0.5m + 0.5m = 1m,AD = AC + CD = 0.5m + 0.5m = 1m,所以,$F_{小}'×1$m = G×0.5m,$F_{大}×0.5$m = G×1m,整理可得:$F_{小}'=\frac{1}{2}G$,$F_{大}=2G$,由题意可知,$\Delta F=F_{大}-F_{小}'=2G-\frac{1}{2}G=\frac{3}{2}G = 18$N,解得:G = 12N。

11.(1)是 右 便于测量力臂大小，消除杠杆自重对杠杆平衡的影响
(2)＜
(3)＞ 60

答案： （1）是 右 便于测量力臂大小，消除杠杆自重对杠杆平衡的影响 （2）＜ （3）＞ 60 解析　（1）实验前,杠杆静止,处于平衡状态;此时杠杆不在水平位置,左端向下倾斜,右端上翘,故应向右调节平衡螺母,使杠杆在水平位置平衡,这样做的好处是便于测量力臂大小,消除杠杆自重对杠杆平衡的影响;（2）图1中杠杆左端下沉,实验时杠杆水平平衡,杠杆的重心位于支点左侧,设杠杆的重心到支点的水平距离为L,杠杆自重为$G'$,则水平平衡时,2G·3a + $G'L=F_{1}·4a$,所以,2G·3a ＜ $F_{1}·4a$;（3）弹簧测力计竖直向上拉杠杆时,动力臂是OA,当斜向上拉杠杆时,动力臂变小,阻力和阻力臂的乘积不变,根据杠杆平衡条件知,动力变大,所以弹簧测力计示数大于2.5N;阻力和阻力臂乘积不变,所以动力和动力臂乘积也不变,弹簧测力计量程是5N,最大能提供5N的拉力,设动力臂为$L'$,则2.5N×4a = 5N×$L'$,所以最小的力臂$L' = 2a$,OA = 4a = 2$L'$,所以拉力的方向与竖直方向的最大夹角为90° - 30° = 60°。