《2025年5年中考3年模拟九年级物理全一册苏科版》

8. 起重机将1000 N的重物先竖直向上匀速提升3 m,再悬停6 s,起重机对重物做功情况是 (D)
A.提升过程做了功,悬停过程做了功
B.提升过程不做功,悬停过程不做功
C.提升过程不做功,悬停过程做了功
D.提升过程做了功,悬停过程不做功

答案： 8.D 起重机提升重物的过程中，重物受到起重机向上的拉力的作用，并向上运动了一段距离，所以起重机在提升重物的过程中对重物做了功；在悬停过程中，重物受到起重机向上的拉力的作用，但没有移动距离，所以起重机在悬停过程中对重物不做功，故选D。

9. 在水平地面上有一正方体木箱,小林用水平推力F把木箱向前推,如图甲所示,此过程中,推力F随时间t的变化情况如图乙所示,木箱前进的速度v的大小随时间t的变化情况如图丙所示,在2~3 s内木箱受到的摩擦力为200N；在3~5 s内,推力F对木箱做功400J,重力对木箱做功0J。

答案： 9.答案：200 400 0
解析：由图丙可知，在3~5s内，木箱做匀速直线运动，木箱通过的距离s=vt = 1.0m/s×(5s - 3s)=2m；由图乙可知，在3~5s内，木箱受到的推力为200N，木箱处于平衡状态，受到的滑动摩擦力与推力大小相等，为200N；由于木箱与地面之间接触面粗糙程度与压力不变，木箱受到的滑动摩擦力不变，则2~3s内木箱受到的滑动摩擦力大小为200N；3~5s内，推力F对木箱做功W=Fs = 200N×2m = 400J，木箱在水平地面上做匀速直线运动，在重力的方向上没有移动距离，重力做功为0J。

10. 工人用图中甲、乙两种方法将实心圆柱形铁块缓慢推倒成丙图情况,则$F_1______F_2；$工人用甲、乙两种方法时至少要做的功分别为$W_1$和$W_2,$则$W_1______W_2。$

答案：
10.答案：＜ =
解析：由图可知，按照图甲的方法，支点为B，F₁的力臂为BD，按照图乙的方法，支点为C，F₂的力臂为D'C，阻力为圆柱形铁块的重力G，阻力臂为底面圆的半径，根据杠杆的平衡条件可知，当阻力和阻力臂不变时，动力臂越长，动力越小，因为BD大于D'C，故F₁＜F₂；两种方法使圆柱形铁块倒下都是克服重力做功，铁块重心移动距离相等，故使用甲、乙两种方法，人至少要做的功的大小相等，即W₁ = W₂。

11. 如图1,粗细均匀的木棒AO放置在水平地面上,小明将木棒A端举过头顶,此时对木棒A端的力为100 N,方向竖直向上,此时木棒A端距地面的高度为2 m,已知OA= 10 m,B为木棒的中点,木棒在O点受到的摩擦力忽略不计。求：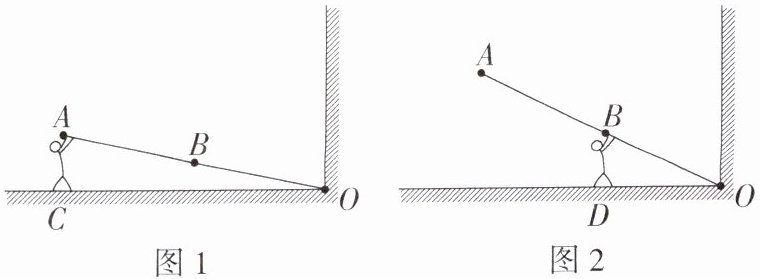
(1)木棒的重力；
(2)如图2,小明缓慢向O点移动,直至将木棒的中点B位置举过头顶,此过程中克服木棒重力做的功。

答案： 11.解析：
(1)图1木棒静止时，B为木棒的中点，动力的方向竖直向上，重力的方向竖直向下，因此动力臂为阻力臂的2倍，即L₁ = 2L₂，此时木棒的重心B点的高度为A端高度的$\frac{1}{2}$，由杠杆平衡条件得$G=\frac{F_{1}L_{1}}{L_{2}}=\frac{100\ \text{N}×2L_{2}}{L_{2}}=200\ \text{N}$；
(2)如图2，将木棒的中点B位置举过头顶时木棒重心上升的高度$\Delta h=h_{B}'-h_{B}=2\ \text{m}-1\ \text{m}=1\ \text{m}$，此过程克服木棒重力做的功$W=G\Delta h=200\ \text{N}×1\ \text{m}=200\ \text{J}$。

12. 航模飞机(图甲)的表演极具观赏性。这种航模飞机需在跑道上加速滑行一段距离,获得足够的升力后才能起飞。已知航模飞机在起飞离地前,平直跑道对它的支持力F₀与滑行距离s的关系如图乙所示。发动机产生的推力为300 N,滑行中获得的升力为$F_1= cv^2,$式中比例系数$c= 7.5 N·s^2/m^2,v$是航模飞机的滑行速度。g取10 N/kg,根据图像解答下列问题：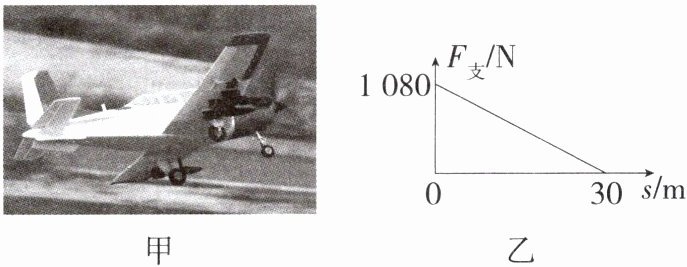
(1)航模飞机的质量为______108______kg,起飞过程中发动机做的功为______9000______J；
(2)航模飞机起飞离地时获得的速度为______12______m/s；
(3)根据航模飞机在竖直方向的受力和图乙的解析式,推导其滑行距离s与滑行速度v之间的关系式：______$s=\frac{5}{24}\ \text{s}^{2}/\text{m}× v^{2}$______。

答案： 12.答案：
(1)108 9000
(2)12
(3)$s=\frac{5}{24}\ \text{s}^{2}/\text{m}× v^{2}$
解析：
(1)根据图乙可知，当飞机静止时，所受重力与支持力平衡，大小相等，即$G=F_{\text{支}}=1080\ \text{N}$，飞机的质量为$m=\frac{G}{g}=\frac{1080\ \text{N}}{10\ \text{N/kg}}=108\ \text{kg}$；根据图乙可知，飞机起飞前的滑行距离为s = 30m，飞机发动机做的功为W = Fs = 300N×30m = 9000J。
(2)飞机刚好离地时，平直跑道对它的支持力为0，获得的升力大小等于飞机的重力大小，即$F_{\text{升}}=G = 1080\ \text{N}$，由$F_{\text{升}}=cv^{2}$可得，飞机的速度为$v=\sqrt{\frac{F_{\text{升}}}{c}}=\sqrt{\frac{1080\ \text{N}}{7.5\ \text{N}\cdot\text{s}^{2}/\text{m}^{2}}}=12\ \text{m/s}$。
(3)由图乙可知$F_{\text{支}}$和s呈线性关系，当s = 0m时，$F_{\text{支}}=1080\ \text{N}$；当s = 30m时，$F_{\text{支}}=0\ \text{N}$，可得$F_{\text{支}}$与滑行距离s间的关系式为$F_{\text{支}}=-36\ \text{N/m}× s+1080\ \text{N}$；滑行过程中飞机在竖直方向的受力大小关系为$G=F_{\text{升}}+F_{\text{支}}$，结合关系式$F_{\text{升}}=cv^{2}$可得，$1080\ \text{N}=cv^{2}+(-36\ \text{N/m}× s+1080\ \text{N})$，代入$c=7.5\ \text{N}\cdot\text{s}^{2}/\text{m}^{2}$可得，滑行距离s与滑行速度v之间的关系式为$s=\frac{5}{24}\ \text{s}^{2}/\text{m}× v^{2}$。