《2025年长江暑假作业崇文书局四年级数学北师大版》

7. 下图是一个等腰三角形的玩具零件示意图,已知$∠1= ∠2$,$∠3= ∠4$,求x的度数。

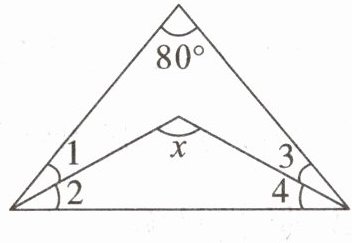
答案： 本题可根据等腰三角形的性质以及三角形内角和定理来求解$x$的度数。
因为$\angle1 = \angle2$，$\angle3 = \angle4$，在等腰三角形中，根据三角形内角和为$180^{\circ}$，可得：
$\angle1+\angle2+\angle3+\angle4+80^{\circ}=180^{\circ}$
$2\angle2 + 2\angle4+80^{\circ}=180^{\circ}$
$2(\angle2 + \angle4)=180^{\circ}-80^{\circ}$
$2(\angle2 + \angle4)=100^{\circ}$
$\angle2 + \angle4 = 100^{\circ}÷2$
$\angle2 + \angle4 = 50^{\circ}$
又因为$x+\angle2+\angle4 = 180^{\circ}$，
所以$x=180^{\circ}-(\angle2 + \angle4)=180^{\circ}- 50^{\circ}=130^{\circ}$。
答案：$x = 130$。

8. 王爷爷有一块菜地的形状近似为等边三角形。如果在菜地的外面围上一圈篱笆,这个篱笆的周长大约是多少？

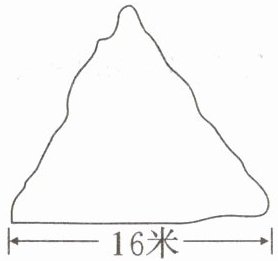
答案： 解析：本题考查的是等边三角形的性质。由于三角形为等边三角形，根据等边三角形的性质：三条边相等，三个角都等于60度，所以篱笆的周长为三条边的长度之和，即：
$16+16+16=48$（米）。
答案：篱笆周长：$16+16+16=48$（米）。

9. 一个农民在自行车的两边分别带着5只鸡和4只兔子去赶集。因为兔子比鸡重,他把鸡和兔子互相交换了一只后,两边的重量就相等了。如果每只兔子重3千克,每只鸡重多少千克？

答案： 解析：本题考查的是列方程解决实际问题。
设每只鸡重x千克。
已知一个农民在自行车的两边分别带着5只鸡和4只兔子去赶集，兔子比鸡重，他把鸡和兔子互相交换了一只后，两边的重量就相等了。
所以，可得：
4x+3=3×3+x
解方程：4x+3=9+x
化简得：3x=6。
解得：x=2。
答案：每只鸡重2千克。