第64页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
一个书包的价格是 42 元,一个笔袋的价格是它的$\frac {1}{3}$,一个笔袋的价格是( )元。
答案:
14
典型例题 学校餐厅运来了$\frac {1}{4}t$蔬菜,第一天用去了这些蔬菜的$\frac {1}{2}$,第二天用去了这些蔬菜的$\frac {3}{8}$。第一天和第二天各用去了多少吨蔬菜?
过程探究
1. 理解题意并列式。
把运来的蔬菜的总质量看作单位“1”,求第一天用去了多少吨蔬菜,就是求$\frac {1}{4}t$的$\frac {1}{2}$是多少,列式为$\frac {1}{4}×\frac {1}{2}$;求第二天用去了多少吨蔬菜,就是求$\frac {1}{4}t$的$\frac {3}{8}$是多少,列式为$\frac {1}{4}×\frac {3}{8}$。
2. 借助示意图理解算式的算理。
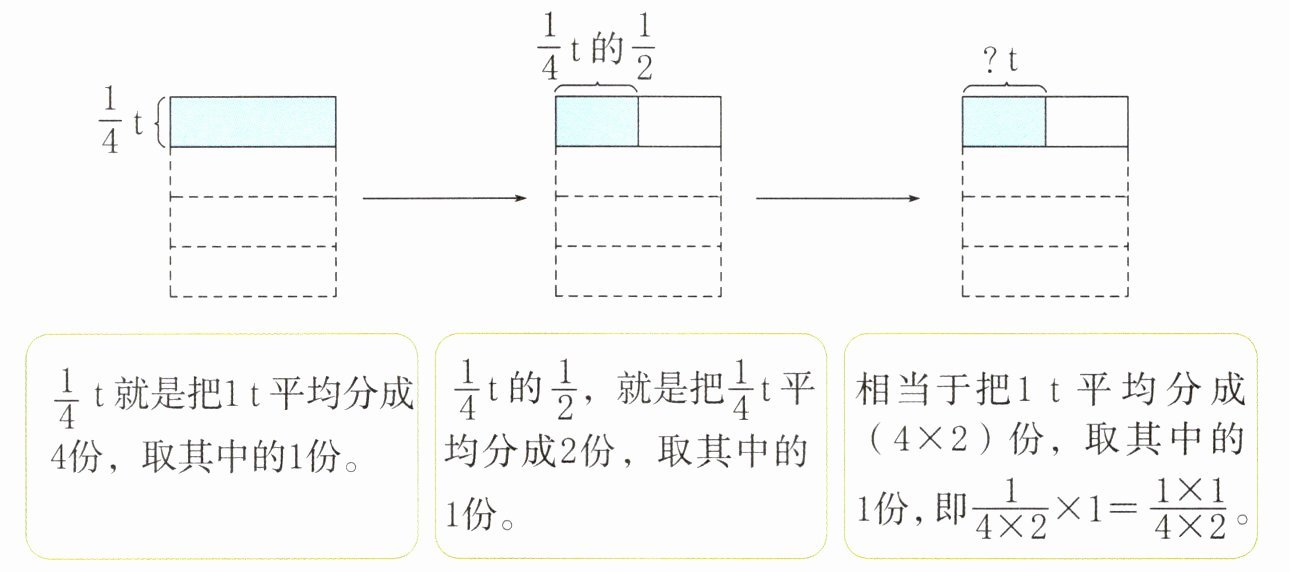
同理,$\frac {1}{4}×\frac {3}{8}=\frac {()×()}{()×()}=\frac {()}{()}(t)$。
通过分析可知,求一个数的几分之几是多少,就用这个数乘几分之几。分数乘分数,用分子相乘的积作( ),用分母相乘的积作( )。
规范解答
过程探究
1. 理解题意并列式。
把运来的蔬菜的总质量看作单位“1”,求第一天用去了多少吨蔬菜,就是求$\frac {1}{4}t$的$\frac {1}{2}$是多少,列式为$\frac {1}{4}×\frac {1}{2}$;求第二天用去了多少吨蔬菜,就是求$\frac {1}{4}t$的$\frac {3}{8}$是多少,列式为$\frac {1}{4}×\frac {3}{8}$。
2. 借助示意图理解算式的算理。

同理,$\frac {1}{4}×\frac {3}{8}=\frac {()×()}{()×()}=\frac {()}{()}(t)$。
通过分析可知,求一个数的几分之几是多少,就用这个数乘几分之几。分数乘分数,用分子相乘的积作( ),用分母相乘的积作( )。
规范解答
答案:
过程探究
2. $\frac{1×3}{4×8}$ $\frac{3}{32}$ 分子 分母
规范解答
$\frac{1}{4}×\frac{1}{2}=\frac{1}{8}(t)$ $\frac{1}{4}×\frac{3}{8}=\frac{3}{32}(t)$
答:第一天用去了$\frac{1}{8}t$蔬菜,第二天用去了$\frac{3}{32}t$蔬菜。
2. $\frac{1×3}{4×8}$ $\frac{3}{32}$ 分子 分母
规范解答
$\frac{1}{4}×\frac{1}{2}=\frac{1}{8}(t)$ $\frac{1}{4}×\frac{3}{8}=\frac{3}{32}(t)$
答:第一天用去了$\frac{1}{8}t$蔬菜,第二天用去了$\frac{3}{32}t$蔬菜。
查看更多完整答案,请扫码查看


