第13页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
5. (推理法解决因数问题)小本暑假到爷爷的牛场去玩。小本问:“爷爷,这群奶牛有多少头?”爷爷说:“这群奶牛,4 头 4 头地数,多 3 头;6 头 6 头地数,多 1 头;7 头 7 头地数,多 2 头。而且这群奶牛的数量在 60 头和 90 头之间。”请你计算一下,这群奶牛有多少头? (12★)
答案:
$7×9 + 2 = 65$ $7×10 + 2 = 72$
$7×11 + 2 = 79$ $7×12 + 2 = 86$
$65÷4 = 16……1$
65不符合题意。
$72÷4 = 18$
72不符合题意。
$79÷4 = 19……3$ $79÷6 = 13……1$
79符合题意。
$86÷4 = 21……2$
86不符合题意。
答:这群奶牛有79头。
$7×11 + 2 = 79$ $7×12 + 2 = 86$
$65÷4 = 16……1$
65不符合题意。
$72÷4 = 18$
72不符合题意。
$79÷4 = 19……3$ $79÷6 = 13……1$
79符合题意。
$86÷4 = 21……2$
86不符合题意。
答:这群奶牛有79头。
6. (列表法解决倍数问题)一个五位数 $\overline{29ABC}$(各位上的数字互不相同)同时是 2、5、3 的倍数,这个五位数可能是多少? (12★)
答案:
因为 $\overline{29ABC}$ 是2和5的倍数,所以个位上的数字是0,即C是0。
因为 $\overline{29ABC}$ 是3的倍数,所以 $2 + 9 + A + B + C$ 是3的倍数,即 $2 + 9 + A + B + 0$ 是3的倍数。
因为 $\overline{29ABC}$ 各位上的数字互不相同,所以 $14 < 2 + 9 + A + B + 0 < 27$。
A和B所代表的数字情况如下表。
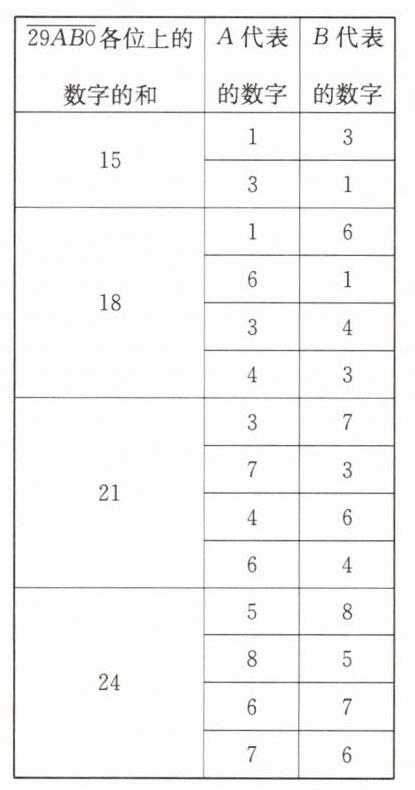
答:这个五位数可能是29130,29310,29160,29610,29340,29430,29370,29730,29460,29640,29580,29850,29670,29760。
因为 $\overline{29ABC}$ 是2和5的倍数,所以个位上的数字是0,即C是0。
因为 $\overline{29ABC}$ 是3的倍数,所以 $2 + 9 + A + B + C$ 是3的倍数,即 $2 + 9 + A + B + 0$ 是3的倍数。
因为 $\overline{29ABC}$ 各位上的数字互不相同,所以 $14 < 2 + 9 + A + B + 0 < 27$。
A和B所代表的数字情况如下表。

答:这个五位数可能是29130,29310,29160,29610,29340,29430,29370,29730,29460,29640,29580,29850,29670,29760。
7. (组数问题)用 1~9 这 9 个数字组成 100 以内的质数。如果每个数字都用到,并且只能用一次,那么这 9 个数字最多能组成几个质数? 分别是多少? (14★)
答案:
这9个数字最多能组成6个质数,分别是2,3,5,41,67,89。(组成的质数不唯一)
8. (推理法解决最多问题)有 20 个自然数,其中奇数比偶数多,这 20 个自然数的总和是 100,那么这 20 个自然数中最多有几个偶数? (14★)
答案:
这20个自然数的总和100是偶数,由于偶数与偶数的和一定是偶数,那么这20个自然数中所有奇数的和必定是偶数,所以一定有偶数个奇数。又因为奇数比偶数多,则奇数最少有12个,所以这20个自然数中最多有8个偶数。
查看更多完整答案,请扫码查看


