《2025年通城学典初中数学运算能手七年级上册苏科版》

11. (24分)去括号,并合并同类项：
(1)$-3(2s-5)+6s$ (2)$3x-\left[5x-\left(\frac{1}{2}x-4\right)\right]$
(3)$2(3a^{2}-2ab)-4\left(-2a^{2}+\frac{1}{3}ab\right)$ (4)$-3(2x^{2}y-xy)+4(yx^{2}+xy-1)$

答案： （1）15 （2）$-\frac{3}{2}x-4$ （3）$14a^{2}-\frac{16}{3}ab$ （4）$-2x^{2}y+7xy-4$

12. (8分)求代数式$a^{2}+1+8a+2a^{2}-9a-3a^{2}-4$的值,其中$a= -3$。

答案： 原式$=-a-3$.当$a=-3$时,原式$=0$

13. (14分)代数式$5a^{3}-4a^{3}b+7a^{2}b+2a^{3}+4a^{3}b-7a^{2}b-7a^{3}+1的值与字母a$,$b$的取值有关吗？为什么？

答案： 无关 因为原式$=(5+2-7)a^{3}+(-4+4)a^{3}b+(7-7)a^{2}b+1=1$,所以代数式$5a^{3}-4a^{3}b+7a^{2}b+2a^{3}+4a^{3}b-7a^{2}b-7a^{3}+1$的值与字母$a,b$的取值无关

14. (14分)有一个数值转换器,其原理如图所示。若开始输入$x$的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,第3次输出的结果是3,按照这种方式,第209次输出的结果是多少？

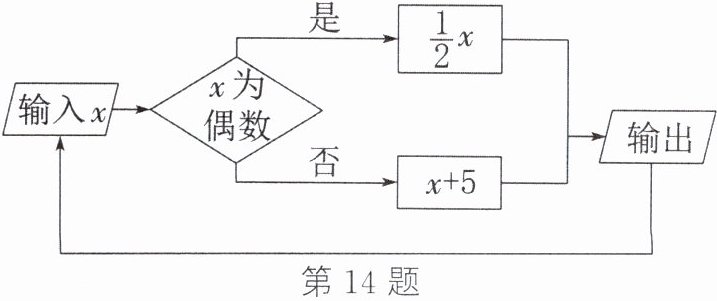
答案： 由题图可知,开始输入$x$的值是7,可发现第1次输出的结果是$7+5=12$,依次计算第1～8次输出的结果,归纳总结得到输出的结果从第2次开始以6,3,8,4,2,1这6个数为一组循环.因为$(209-1)÷6=34\cdots\cdots4$,所以第209次输出的结果是4