《2025年思维新观察八年级数学上册人教版》

23.(10分)如图,等腰$\text{Rt}\triangle ACB$中,$∠ACB=90^{\circ },∠CAB=∠CBA=45^{\circ },AC=BC,E$点为射线$CB$上一动点,连接$AE$,作$AF⊥AE$且$AF=AE$.
(1)如图1,过$F$点作$FG⊥AC$交$AC$于$G$点,求证:$\triangle AGF\cong \triangle ECA$(AAS);
(2)如图2,在(1)的条件下,连接$BF$交$AC$于$D$点,若$AD=3CD$,求证:$E$点为$BC$中点;
(3)如图3,当$E$点在$CB$的延长线上时,连接$BF$与$AC$的延长线交于$D$点,
若$\frac {BC}{BE}=\frac {4}{3}$,则$\frac {AD}{CD}=$$\frac{11}{3}$.

答案： 证明:
(1)
∵∠FAG+∠CAE=90°,
∠FAG+∠GFA=90°,
∴∠CAE=∠GFA,在△AGF和△ECA中,
{∠AGF=∠ECA
∠GFA=∠CAE
AF=AE,
∴△AGF≌△ECA(AAS);
(2)由
(1)知△AGF≌△ECA,
∴FG=AC=BC,
在△FGD和△BCD中,
{∠FDG=∠BDC
∠FGD=∠BCD=90°
FG=BC,
∴△FGD≌△BCD(AAS),
∴DG=CD,
∵AD/CD=3,
∴AG/CD=2,
∴AG/AC=1/2,
∵AG=CE,AC=BC,
∴CE/BC=1/2,
∴E点为BC中点;
(3)过F作FG⊥AD的延长线交于点G,
∵BC/BE=4/3,
BC=AC,CE=CB+BE,
∴AC/CE=4/7,由
(1)
(2)知:
△AGF≌△ECA,△DGF≌△DCB,
∴CD=DG,AG=CE,
∴AC/AG=4/7,
∴AC/CG=4/3,
∴
AC/(1/2 CG)=AC/CD=8/3,
∴AD/CD=11/3.

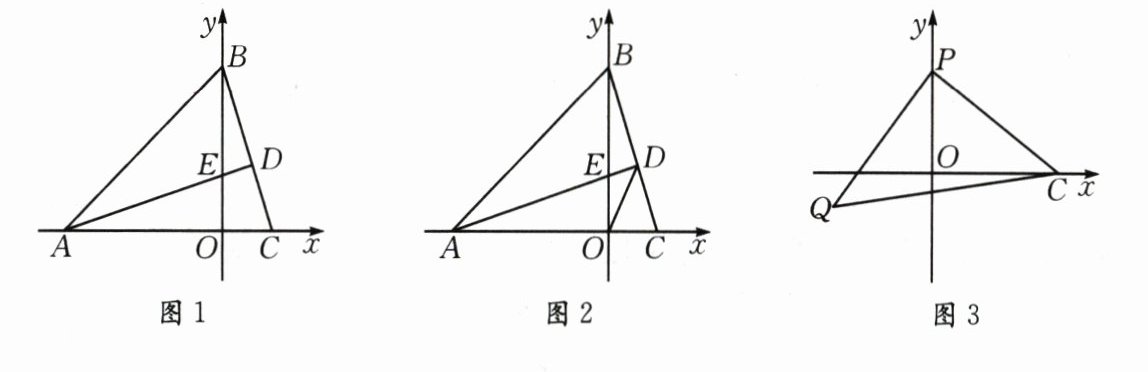
24.(12分)如图1,在平面直角坐标系中,$\triangle ABC$的顶点$A(-3,0),B(0,3),AD⊥BC$交$BC$于$D$点,交$y$轴正半轴于点$E(0,t)$.
(1) 当$t=1$时,求$C$点的坐标;
(2) 如图2,求$∠ADO$的度数;
(3) 如图3,已知点$P(0,2)$.若$PQ⊥PC,PQ=PC$,求$Q$的坐标(用含$t$的式子表示).

答案：
(1)AD⊥BC,
∴∠EAO+∠BCO=90°,
∵∠CBO+∠BCO=90°,
∴∠EAO=∠CBO,
在△AOE和△BOC中,
{∠EAO=∠CBO
AO=BO
∠AOE=∠BOC=90°,
∴△AOE≌△BOC,
∴OE=OC=1,
∴点C坐标(1,0);
(2)过点O作OM⊥AD于点M,作ON⊥BC于点N,
∵△AOE≌△BOC,S△AOE=S△BOC,AE=BC,
∵OM⊥AE,ON⊥BC,
∴OM=ON,
∴OD平分∠ADC,
∴∠ADO=1/2∠ADC=45°;
(3)过点Q作QR垂直于x轴于R,作PM⊥QR于M点,由
(1)知点C的坐标为(t,0),四边形PMRO为矩形,
∠QPM+∠QPO=∠QPO+∠CPO,
∴∠QPM=∠CPO,
在△QPM和△CPO中,
{∠PMQ=∠POC
∠QPM=∠CPO⇒△QPM≌△CPO,
PQ=PC
∴PM=PO=2,QM=CO=t,
∴点Q坐标是(-2,2-t).