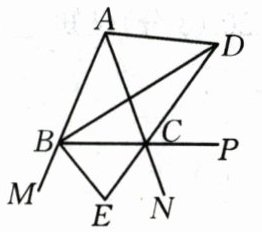
10. 如图, ∠ABC=∠ACB, BD, CD, BE分别平分∠ABC, 外角∠ACP, 外角∠MBC, 以下结论: ①AD//BC; ②DB⊥BE; ③∠BDC+∠ABC=90°; ④∠BAC+2∠BEC=180°; ⑤DB平分∠ADC, 其中正确的结论有(
A. 2个
B. 3个
C. 4个
D. 5个
C
)
A. 2个
B. 3个
C. 4个
D. 5个
答案:
10.C
11. 在△ABC中, ∠A是∠B的2倍, ∠C比∠A+∠B还大12°, 则这个三角形是______三角形.
钝角
答案:
11.钝角
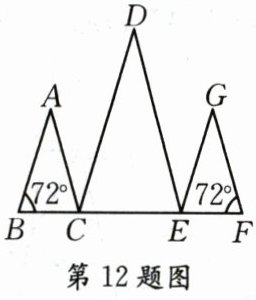
12. 如图, 点B, C, E, F在一直线上, AB//DC, DE//GF, ∠B=∠F=72°, 则∠D=
36
度.
答案:
12.36
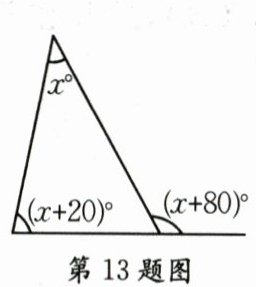
13. 如图, x=
60
.
答案:
13.60
14. 等腰三角形的两边长为6cm, 13cm, 则它的周长是______
32 cm
.
答案:
14.32 cm
15. 一幅三角板△ABC, △ADE, 如图放置. 则∠1, ∠2, α之间关系为
∠1-∠2+α=105°
.
答案:
15.$\angle 1-\angle 2+\alpha =105^{\circ }$
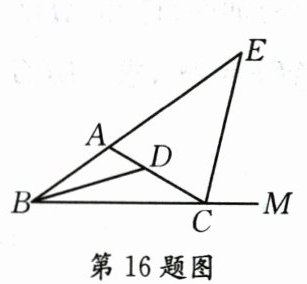
16. 如图所示, △ABC中, BD平分∠ABC, CE平分∠ACB的邻补角∠ACM, 若∠BDC=130°, ∠E=50°, 则∠BAC的度数是______
120°
.
答案:
16.$120^{\circ }$
17. (8分)用一条长为18cm的细绳围成一个等腰三角形, 如果腰长是底边长的2倍, 那么各边的长是多少?
答案:
17.设底边长为$x$ cm,则腰长为$2x$ cm.
$x+2x+2x=18$,解得$x=3.6$.
答:三边长分别为$3.6$ cm,$7.2$ cm,$7.2$ cm.
$x+2x+2x=18$,解得$x=3.6$.
答:三边长分别为$3.6$ cm,$7.2$ cm,$7.2$ cm.
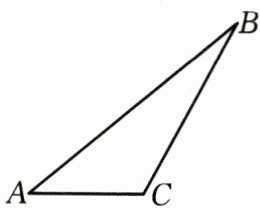
18. (8分)如图, 钝角△ABC.
(1)过A作AE⊥BC, 过B作BF⊥AC, 垂足分别为E, F, AE, BF相交于H;
(2)过A作AM//BC, 过B作BM//AC, 相交于M;
(3)若∠AMB=115°, 求∠AHB.
(1)过A作AE⊥BC, 过B作BF⊥AC, 垂足分别为E, F, AE, BF相交于H;
(2)过A作AM//BC, 过B作BM//AC, 相交于M;
(3)若∠AMB=115°, 求∠AHB.

答案:
1. 首先,证明四边形$AMBC$是平行四边形:
已知$AM// BC$,$BM// AC$,根据平行四边形的定义(两组对边分别平行的四边形是平行四边形),所以四边形$AMBC$是平行四边形。
那么$\angle C=\angle AMB$(平行四边形的对角相等)。
因为$\angle AMB = 115^{\circ}$,所以$\angle C = 115^{\circ}$。
2. 然后,在四边形$CEHF$中:
因为$AE\perp BC$,$BF\perp AC$,所以$\angle HEC = 90^{\circ}$,$\angle HFC = 90^{\circ}$。
根据四边形内角和公式$\angle HEC+\angle HFC+\angle C+\angle EHF = 360^{\circ}$($n$边形内角和公式$(n - 2)×180^{\circ}$,这里$n = 4$,$(4 - 2)×180^{\circ}=360^{\circ}$)。
把$\angle HEC = 90^{\circ}$,$\angle HFC = 90^{\circ}$,$\angle C = 115^{\circ}$代入上式得:$90^{\circ}+90^{\circ}+115^{\circ}+\angle EHF = 360^{\circ}$。
则$\angle EHF=360^{\circ}-(90^{\circ}+90^{\circ}+115^{\circ})=65^{\circ}$。
3. 最后,求$\angle AHB$:
因为$\angle AHB$与$\angle EHF$是对顶角,根据对顶角相等($\angle AHB$和$\angle EHF$是对顶角,对顶角的定义:如果一个角的两边分别是另一个角两边的反向延长线,且这两个角有公共顶点,那么这两个角是对顶角),$\angle AHB=\angle EHF$。
所以$\angle AHB = 65^{\circ}$。
已知$AM// BC$,$BM// AC$,根据平行四边形的定义(两组对边分别平行的四边形是平行四边形),所以四边形$AMBC$是平行四边形。
那么$\angle C=\angle AMB$(平行四边形的对角相等)。
因为$\angle AMB = 115^{\circ}$,所以$\angle C = 115^{\circ}$。
2. 然后,在四边形$CEHF$中:
因为$AE\perp BC$,$BF\perp AC$,所以$\angle HEC = 90^{\circ}$,$\angle HFC = 90^{\circ}$。
根据四边形内角和公式$\angle HEC+\angle HFC+\angle C+\angle EHF = 360^{\circ}$($n$边形内角和公式$(n - 2)×180^{\circ}$,这里$n = 4$,$(4 - 2)×180^{\circ}=360^{\circ}$)。
把$\angle HEC = 90^{\circ}$,$\angle HFC = 90^{\circ}$,$\angle C = 115^{\circ}$代入上式得:$90^{\circ}+90^{\circ}+115^{\circ}+\angle EHF = 360^{\circ}$。
则$\angle EHF=360^{\circ}-(90^{\circ}+90^{\circ}+115^{\circ})=65^{\circ}$。
3. 最后,求$\angle AHB$:
因为$\angle AHB$与$\angle EHF$是对顶角,根据对顶角相等($\angle AHB$和$\angle EHF$是对顶角,对顶角的定义:如果一个角的两边分别是另一个角两边的反向延长线,且这两个角有公共顶点,那么这两个角是对顶角),$\angle AHB=\angle EHF$。
所以$\angle AHB = 65^{\circ}$。
19. (8分)利用无刻度直尺作图.
(1)如图1, A, B在格点上, 作一个格点C, 使△ABC面积为5;
(2)如图2, A, B, C在格点上, 作格点D, 使四边形ABCD面积为7.5;
(3)如图3, 在4×4的网格上, A, B为格点, 找出所有格点C, 使$S_{△ABC}=1.$

(1)如图1, A, B在格点上, 作一个格点C, 使△ABC面积为5;
(2)如图2, A, B, C在格点上, 作格点D, 使四边形ABCD面积为7.5;
(3)如图3, 在4×4的网格上, A, B为格点, 找出所有格点C, 使$S_{△ABC}=1.$

答案:
1. (1)
解:设$A(x_1,y_1)$,$B(x_2,y_2)$,根据三角形面积公式$S = \frac{1}{2}×底×高$。
已知$A$,$B$在格点上,若以$AB$为底,设$AB$的水平距离为$a$,垂直距离为$b$,$S_{\triangle ABC}=\frac{1}{2}× AB× h = 5$。
假设$AB$横向占$4$个单位长度,纵向占$2$个单位长度(可通过勾股定理算$AB$长度,但这里用面积关系),我们可以让$C$到$AB$的距离$h=\frac{5×2}{AB}$(这里用等积法思路)。
一种方法:将$A$向上平移$2$个单位,再向右平移$1$个单位得到$C$(答案不唯一)。
2. (2)
解:先计算$\triangle ABC$的面积,设$A(x_1,y_1)$,$B(x_2,y_2)$,$C(x_3,y_3)$,根据$S=\frac{1}{2}\left|x_1(y_2 - y_3)+x_2(y_3 - y_1)+x_3(y_1 - y_2)\right|$(格点三角形面积也可用割补法)。
假设$\triangle ABC$面积为$S_1$,设$S_{ABCD}=S_1 + S_{\triangle ABD}=7.5$。
先算出$\triangle ABC$面积(用割补法:$\triangle ABC$占$3$个小正方形,面积$S_{\triangle ABC}= 3$),则$S_{\triangle ABD}=7.5 - 3=4.5$。
把$B$向上平移$3$个单位,再向右平移$1$个单位得到$D$(答案不唯一)。
3. (3)
解:设$A(x_1,y_1)$,$B(x_2,y_2)$,根据$S_{\triangle ABC}=\frac{1}{2}×底×高 = 1$。
若以$AB$为底,设$AB$的水平距离为$m$,垂直距离为$n$,$S=\frac{1}{2}\sqrt{m^{2}+n^{2}}× h = 1$(这里也可用格点关系)。
当$AB$横向距离为$2$,纵向距离为$1$时:
过$A$作与$AB$垂直且距离为$\frac{2×1}{\sqrt{2^{2}+1^{2}}}$(根据面积公式$S = \frac{1}{2}× AB× h$,$AB=\sqrt{5}$,$h=\frac{2}{\sqrt{5}}$,通过格点关系找),符合条件的$C$点有$6$个(分别在$A$,$B$所在直线的两侧,通过上下左右平移$1$个单位等方式得到)。
(1)、(2)题答案不唯一,(3)题符合条件的格点$C$有$6$个。
解:设$A(x_1,y_1)$,$B(x_2,y_2)$,根据三角形面积公式$S = \frac{1}{2}×底×高$。
已知$A$,$B$在格点上,若以$AB$为底,设$AB$的水平距离为$a$,垂直距离为$b$,$S_{\triangle ABC}=\frac{1}{2}× AB× h = 5$。
假设$AB$横向占$4$个单位长度,纵向占$2$个单位长度(可通过勾股定理算$AB$长度,但这里用面积关系),我们可以让$C$到$AB$的距离$h=\frac{5×2}{AB}$(这里用等积法思路)。
一种方法:将$A$向上平移$2$个单位,再向右平移$1$个单位得到$C$(答案不唯一)。
2. (2)
解:先计算$\triangle ABC$的面积,设$A(x_1,y_1)$,$B(x_2,y_2)$,$C(x_3,y_3)$,根据$S=\frac{1}{2}\left|x_1(y_2 - y_3)+x_2(y_3 - y_1)+x_3(y_1 - y_2)\right|$(格点三角形面积也可用割补法)。
假设$\triangle ABC$面积为$S_1$,设$S_{ABCD}=S_1 + S_{\triangle ABD}=7.5$。
先算出$\triangle ABC$面积(用割补法:$\triangle ABC$占$3$个小正方形,面积$S_{\triangle ABC}= 3$),则$S_{\triangle ABD}=7.5 - 3=4.5$。
把$B$向上平移$3$个单位,再向右平移$1$个单位得到$D$(答案不唯一)。
3. (3)
解:设$A(x_1,y_1)$,$B(x_2,y_2)$,根据$S_{\triangle ABC}=\frac{1}{2}×底×高 = 1$。
若以$AB$为底,设$AB$的水平距离为$m$,垂直距离为$n$,$S=\frac{1}{2}\sqrt{m^{2}+n^{2}}× h = 1$(这里也可用格点关系)。
当$AB$横向距离为$2$,纵向距离为$1$时:
过$A$作与$AB$垂直且距离为$\frac{2×1}{\sqrt{2^{2}+1^{2}}}$(根据面积公式$S = \frac{1}{2}× AB× h$,$AB=\sqrt{5}$,$h=\frac{2}{\sqrt{5}}$,通过格点关系找),符合条件的$C$点有$6$个(分别在$A$,$B$所在直线的两侧,通过上下左右平移$1$个单位等方式得到)。
(1)、(2)题答案不唯一,(3)题符合条件的格点$C$有$6$个。
查看更多完整答案,请扫码查看


