23. (10分)如图1,在$\triangle ABC$中,$AB = AC$,$\angle BAC = 30^{\circ}$,点$D$是$\triangle ABC$内一点,$DB = DC$,$\angle DCB = 30^{\circ}$,点$E$是$BD$延长线上一点,$AE = AB$.
(1)直接写出$\angle ADE$的度数____
(2)求证:$DE = AD + DC$;
(3)作$BP$平分$\angle ABE$,$EF\perp BP$,垂足为$F$(如图2),若$EF = 3$,求$BP$的长.
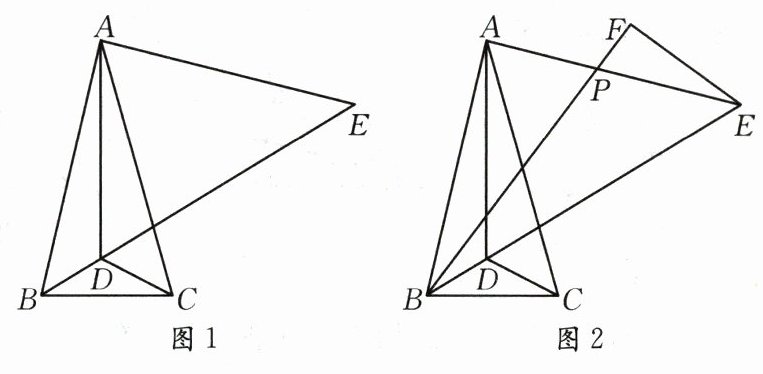
(1)直接写出$\angle ADE$的度数____
60°
;(2)求证:$DE = AD + DC$;
(3)作$BP$平分$\angle ABE$,$EF\perp BP$,垂足为$F$(如图2),若$EF = 3$,求$BP$的长.
6

答案:
(1)$60^{\circ}$;
(2)在DE上取一点M,使$AD = DM$,连接AM,则$△ABD≌△AEM$,
∴$BD = EM$,
∴$DE = DM + ME = AD + BD = AD + DC$;
(3)延长EF交BA的延长线于N点,易证$BP = EN = 2EF = 6$。
(1)$60^{\circ}$;
(2)在DE上取一点M,使$AD = DM$,连接AM,则$△ABD≌△AEM$,
∴$BD = EM$,
∴$DE = DM + ME = AD + BD = AD + DC$;
(3)延长EF交BA的延长线于N点,易证$BP = EN = 2EF = 6$。
24. (12分)如图1,$A$是$OB$的垂直平分线上一点,$P$为$y$轴上一点且$\angle OPB=\angle OAB$.
(1)若$\angle AOB = 60^{\circ}$,$PB = 4$,求点$P$的坐标;
(2)在(1)的条件下,求证:$PA + PO = PB$;
(3)如图2,若点$A$是$OB$的垂直平分线上一点,已知$A(2,5)$,$\angle OPB=\angle OAB$,求$PO + PB$的值.
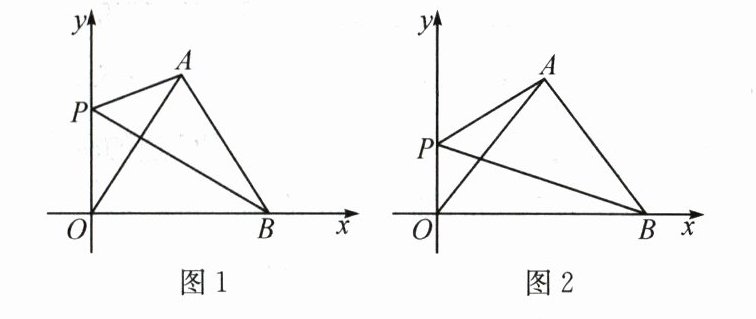
(1)若$\angle AOB = 60^{\circ}$,$PB = 4$,求点$P$的坐标;
(2)在(1)的条件下,求证:$PA + PO = PB$;
(3)如图2,若点$A$是$OB$的垂直平分线上一点,已知$A(2,5)$,$\angle OPB=\angle OAB$,求$PO + PB$的值.

答案:
(1)P点坐标为$(0, 2)$;
(2)在PB上取一点E,使$OP = OE$,
在$△POA$和$△EOB$中,
$\begin{cases}OP = OE \\ ∠POA = ∠EOB \\ OA = OB \end{cases}$,
∴$△POA≌△EOB(SAS)$,
∴$PA = EB$,
∴$PB = PE + EB = PO + PA$;
(3)延长BA交y轴于点D,过A作$AH⊥x$轴,$AE⊥y$轴,
∵$OA = AB$,$∠AOB = ∠ABO$,
∵$∠ABO + ∠ODB = ∠AOB + ∠AOD = 90^{\circ}$,
∴$∠AOD = ∠ODB$,
∴$∠ODB = ∠ABP$,
∴$AD = OA$,$BP = PD$,
∴E为OD中点,
∵$OE = AH = 5$,
∴$PO + PB = PO + PD = OD = 2OE = 10$。
(1)P点坐标为$(0, 2)$;
(2)在PB上取一点E,使$OP = OE$,
在$△POA$和$△EOB$中,
$\begin{cases}OP = OE \\ ∠POA = ∠EOB \\ OA = OB \end{cases}$,
∴$△POA≌△EOB(SAS)$,
∴$PA = EB$,
∴$PB = PE + EB = PO + PA$;
(3)延长BA交y轴于点D,过A作$AH⊥x$轴,$AE⊥y$轴,
∵$OA = AB$,$∠AOB = ∠ABO$,
∵$∠ABO + ∠ODB = ∠AOB + ∠AOD = 90^{\circ}$,
∴$∠AOD = ∠ODB$,
∴$∠ODB = ∠ABP$,
∴$AD = OA$,$BP = PD$,
∴E为OD中点,
∵$OE = AH = 5$,
∴$PO + PB = PO + PD = OD = 2OE = 10$。
查看更多完整答案,请扫码查看


