11.在$△ABC$中,$∠C=90^{\circ },∠A$比$∠B$大$20^{\circ }$,则$∠B=$
$35^{\circ}$
.
答案:
$35^{\circ}$
12.在$△ABC$中,$AB=5,AC=3,BC=x$,则x的范围为
$2 < x < 8$
.
答案:
$2 < x < 8$
13.在正n边形中,每个角为$135^{\circ }$,则边数n为
8
.
答案:
8
14.已知$△ABC$中,$AB=10,AC=6,BC=8$,若三条内角平分线交于点O,$OG⊥AB$于G,则AG的长度为
4
.
答案:
4
15.如图,小亮从A点出发前进10 m,向右转$15^{\circ }$,再前进10 m,又向右转$15^{\circ }$……这样一直走下去,他第一次回到出发点A时,一共走了
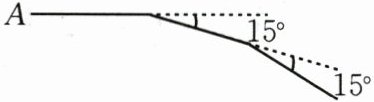
240
m.
答案:
240
16.如图,在平面直角坐标系中,点$C(0,4),E(-4,0)$,点A为线段CE上一动点,以AO为斜边作等腰直角$△AOB$(点A,O,B以顺时针排列)点D在射线BO上,若以点D,C,O构成三角形和$△AOC$全等,则$∠CAO=$
$45^{\circ}$或$67.5^{\circ}$
.
答案:
$45^{\circ}$或$67.5^{\circ}$
17.(8分)如图,D,E分别是AB,AC上的点,且$AB=AC,AD=AE$.求证:$∠B=∠C$.
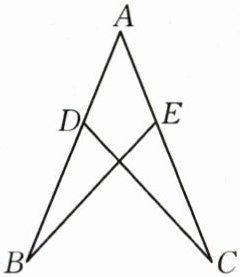

答案:
【解析】:
在$\triangle ABE$和$\triangle ACD$中,
$\begin{cases}AB = AC \\ \angle A=\angle A\\AE = AD\end{cases}$(已知条件)
根据全等三角形判定定理中的“边角边”($SAS$),可得$\triangle ABE\cong\triangle ACD$。
因为全等三角形的对应角相等,所以$\angle B=\angle C$。
【答案】:
在$\triangle ABE$和$\triangle ACD$中,$\begin{cases}AB = AC \\ \angle A=\angle A\\AE = AD\end{cases}$,$\therefore\triangle ABE\cong\triangle ACD(SAS)$,$\therefore\angle B=\angle C$。
在$\triangle ABE$和$\triangle ACD$中,
$\begin{cases}AB = AC \\ \angle A=\angle A\\AE = AD\end{cases}$(已知条件)
根据全等三角形判定定理中的“边角边”($SAS$),可得$\triangle ABE\cong\triangle ACD$。
因为全等三角形的对应角相等,所以$\angle B=\angle C$。
【答案】:
在$\triangle ABE$和$\triangle ACD$中,$\begin{cases}AB = AC \\ \angle A=\angle A\\AE = AD\end{cases}$,$\therefore\triangle ABE\cong\triangle ACD(SAS)$,$\therefore\angle B=\angle C$。
18.(8分)如图所示,$∠BAC=∠ABD=90^{\circ },AC=BD$,点O是AD,BC的交点,点E是AB的中点.
(1)图中有哪几对全等三角形?请写出来;
(2)试判断OE和AB的位置关系,并给予证明.
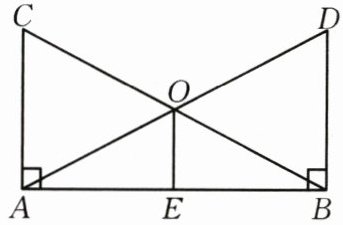
(1)图中有哪几对全等三角形?请写出来;
(2)试判断OE和AB的位置关系,并给予证明.

答案:
(1) $ \triangle A B C \cong \triangle B A D $,$ \triangle A O E \cong \triangle B O E $,$ \triangle A O C \cong \triangle B O D $;
(2) $ O E \perp A B $. 理由如下:
在 $ \mathrm { Rt } \triangle A B C $ 和 $ \mathrm { Rt } \triangle B A D $ 中,$ \left\{ \begin{array} { l } { A C = B D } \\ { \angle B A C = \angle A B D } \\ { A B = B A } \end{array} \right. $,$ \therefore \triangle A B C \cong \triangle B A D ( \mathrm { SAS } ) $,$ \therefore \angle D A B = \angle C B A $,$ \therefore O A = O B $,$ \because $ 点 $ E $ 是 $ A B $ 的中点,$ \therefore O E \perp A B $.
(1) $ \triangle A B C \cong \triangle B A D $,$ \triangle A O E \cong \triangle B O E $,$ \triangle A O C \cong \triangle B O D $;
(2) $ O E \perp A B $. 理由如下:
在 $ \mathrm { Rt } \triangle A B C $ 和 $ \mathrm { Rt } \triangle B A D $ 中,$ \left\{ \begin{array} { l } { A C = B D } \\ { \angle B A C = \angle A B D } \\ { A B = B A } \end{array} \right. $,$ \therefore \triangle A B C \cong \triangle B A D ( \mathrm { SAS } ) $,$ \therefore \angle D A B = \angle C B A $,$ \therefore O A = O B $,$ \because $ 点 $ E $ 是 $ A B $ 的中点,$ \therefore O E \perp A B $.
19.(8分)上午8时,一条船从海岛A出发,以15海里/时的速度向正北航行,10时到达海岛B处,从A,B望灯塔C,测得$∠NAC=43^{\circ },∠NBC=86^{\circ }$,问海岛B与灯塔C相距多远?
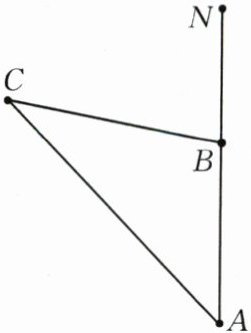

答案:
相距 30 海里
查看更多完整答案,请扫码查看


