23.(10分)(1)图1是由四个全等的直角三角形(边长分别为a,b,c,且$a<b<c$)和一个小正方形拼成的大正方形,利用图1验证公式的方法求出a,b,c满足的等量关系式;
(2)如图1,在(1)的条件下,若$a+b=7,c=5$,求阴影部分的面积;
(3)如图2,以(1)中a,b,c为边作三个正方形,并将以a,b为边的两个小正方形放置于以c为边长的大正方形内,若阴影部分的面积为1,求四边形ABCD的面积.
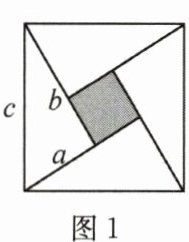

(2)如图1,在(1)的条件下,若$a+b=7,c=5$,求阴影部分的面积;
(3)如图2,以(1)中a,b,c为边作三个正方形,并将以a,b为边的两个小正方形放置于以c为边长的大正方形内,若阴影部分的面积为1,求四边形ABCD的面积.


答案:
解:
(1) $ \because $ 从构成看,大正方形由四个直角三角形和一个小正方形组成
$ \therefore $ 大正方形面积可表示为:$ \frac { 1 } { 2 } a b \times 4 + ( b - a ) ^ { 2 } $
$ \therefore \frac { 1 } { 2 } a b \times 4 + ( b - a ) ^ { 2 } = c ^ { 2 } $,$ \therefore a ^ { 2 } + b ^ { 2 } = c ^ { 2 } $
(2) $ \because c = 5 $,$ \therefore c ^ { 2 } = 25 $,$ \therefore a ^ { 2 } + b ^ { 2 } = 25 $
$ \because a + b = 7 $,$ \therefore ( a + b ) ^ { 2 } = 49 $,$ \therefore 25 + 2 a b = 49 $,$ \therefore 2 a b = 24 $
$ \because S _ { 阴影 } = ( b - a ) ^ { 2 } = a ^ { 2 } + b ^ { 2 } - 2 a b $
$ \therefore S _ { 阴影 } = 25 - 24 = 1 $
(3) $ \because $ 图 3 中两个长方形的边长均为 $ c - a $ 和 $ c - b $
$ \therefore $ 两个长方形的面积相等
$ \therefore S _ { 阴影 } = a ^ { 2 } + b ^ { 2 } + 2 \times S _ { 四边形 A B C D } - c ^ { 2 } $
$ \because a ^ { 2 } + b ^ { 2 } = c ^ { 2 } $,$ S _ { 阴影 } = 1 $,$ \therefore 2 S _ { 四边形 A B C D } = 1 $
$ \therefore S _ { 四边形 A B C D } = 0.5 $
(1) $ \because $ 从构成看,大正方形由四个直角三角形和一个小正方形组成
$ \therefore $ 大正方形面积可表示为:$ \frac { 1 } { 2 } a b \times 4 + ( b - a ) ^ { 2 } $
$ \therefore \frac { 1 } { 2 } a b \times 4 + ( b - a ) ^ { 2 } = c ^ { 2 } $,$ \therefore a ^ { 2 } + b ^ { 2 } = c ^ { 2 } $
(2) $ \because c = 5 $,$ \therefore c ^ { 2 } = 25 $,$ \therefore a ^ { 2 } + b ^ { 2 } = 25 $
$ \because a + b = 7 $,$ \therefore ( a + b ) ^ { 2 } = 49 $,$ \therefore 25 + 2 a b = 49 $,$ \therefore 2 a b = 24 $
$ \because S _ { 阴影 } = ( b - a ) ^ { 2 } = a ^ { 2 } + b ^ { 2 } - 2 a b $
$ \therefore S _ { 阴影 } = 25 - 24 = 1 $
(3) $ \because $ 图 3 中两个长方形的边长均为 $ c - a $ 和 $ c - b $
$ \therefore $ 两个长方形的面积相等
$ \therefore S _ { 阴影 } = a ^ { 2 } + b ^ { 2 } + 2 \times S _ { 四边形 A B C D } - c ^ { 2 } $
$ \because a ^ { 2 } + b ^ { 2 } = c ^ { 2 } $,$ S _ { 阴影 } = 1 $,$ \therefore 2 S _ { 四边形 A B C D } = 1 $
$ \therefore S _ { 四边形 A B C D } = 0.5 $
24.(12分)在平面直角坐标系中,$M(m,n)$且m,n满足$m^{2}+2n^{2}-2mn+4n+4=0,B(0,b)$为y轴上一动点,将直线BM绕B点顺时针旋转$45^{\circ }$交x轴于点C,过C作$AC⊥BC$交直线BM于点$A(a,t)$.
(1)求点M的坐标;
(2)如图1,在B点运动的过程中,A点的横坐标是否会发生变化? 若不变,求a的值;若变化,写出A点的横坐标a的取值范围;
(3)如图2,过$T(a,0)$作$TH⊥BM$(垂足H在x轴下方),在射线HB上截取$HK=HT$,连OK,求$∠OKB$的度数.
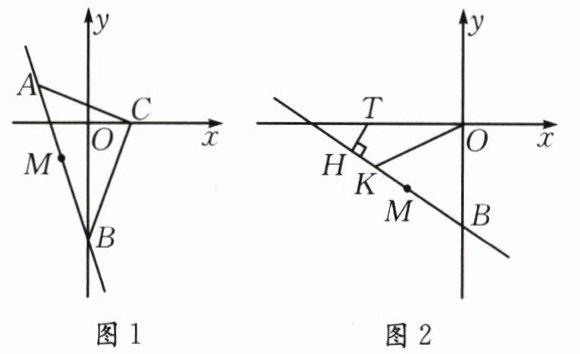
(1)求点M的坐标;
(2)如图1,在B点运动的过程中,A点的横坐标是否会发生变化? 若不变,求a的值;若变化,写出A点的横坐标a的取值范围;
(3)如图2,过$T(a,0)$作$TH⊥BM$(垂足H在x轴下方),在射线HB上截取$HK=HT$,连OK,求$∠OKB$的度数.

答案:
(1) $ \because M ( m, n ) $ 且 m,n 满足 $ m ^ { 2 } + 2 n ^ { 2 } - 2 m n + 4 n + 4 = 0 $
$ \therefore m ^ { 2 } - 2 m n + n ^ { 2 } + n ^ { 2 } + 4 n + 4 = 0 $
$ \therefore ( m - n ) ^ { 2 } + ( n + 2 ) ^ { 2 } = 0 $
$ \therefore m = n = - 2 $,$ \therefore $ 点 M 的坐标为 $ ( - 2, - 2 ) $
(2) 过 A 作 $ A E \perp x $ 轴于 D,交 OM 的延长线于 E
$ \therefore A E // O B $
$ \therefore \angle B O M = \angle A E M $,$ \angle O B M = \angle E A M $
在 $ \mathrm { Rt } \triangle A C B $ 中,$ \angle A C B = 90 ^ { \circ } $,$ \angle A B C = 45 ^ { \circ } $
$ \therefore \triangle A C B $ 为等腰直角三角形
$ \therefore A C = B C $
$ \because \angle A C D + \angle B C O = \angle B C O + \angle C B O = 90 ^ { \circ } $
$ \therefore \angle A C D = \angle C B O $
在 $ \mathrm { Rt } \triangle A D C $ 和 $ \mathrm { Rt } \triangle C O B $ 中
$ \because \angle A D C = \angle C O B = 90 ^ { \circ } $
$ A C = B C $,$ \angle A C D = \angle C B O $
$ \therefore \mathrm { Rt } \triangle A D C \cong \mathrm { Rt } \triangle C O B ( \mathrm { AAS } ) $
$ \therefore C D = B O $,$ A D = C O $
$ \because A ( a, t ) $,$ B ( 0, b ) $
$ \therefore D O = - a $,$ A D = C O = t $,$ C D = B O = - b $
$ \therefore D ( a, 0 ) $,$ C ( t, 0 ) $,$ C D = D O + C O = B O = - b $
$ \therefore t - a = - b $
$ \because M ( - 2, 2 ) $,$ \therefore \angle E O D = \angle B O E = 45 ^ { \circ } $
$ \therefore \triangle E D O $ 为等腰直角三角形
$ \therefore D O = D E = - a $
$ \therefore A E = A D + D E = t - a = - b = O B $
在 $ \triangle A E M $ 和 $ \triangle B O M $ 中
$ \because \angle B O M = \angle A E M $,$ A E = O B $,$ \angle O B M = \angle E A M $
$ \therefore \triangle A E M \cong \triangle B O M ( \mathrm { ASA } ) $
$ \therefore M E = M O $
$ \therefore D E = 2 \times 2 = 4 = D O $
$ \therefore a = - 4 $
(3) $ \angle O K B $ 的度数为 $ 45 ^ { \circ } $
方法 1 (三垂直):连接 TM,OM,作 $ O N \perp M B $,$ M G \perp O T $,垂足分别是 N,G
$ \therefore \angle O N M = \angle O G M = 90 ^ { \circ } $
$ \because M ( - 2, - 2 ) $
$ \therefore \angle B O M = \angle T O M = 45 ^ { \circ } $
$ \therefore \triangle O G M $ 为等腰直角三角形
$ \therefore M G = O G = 2 $
又 $ \because T ( a, 0 ) $,$ a = - 4 $
$ \therefore O T = 4 $,$ \therefore M G = O G = T G = 2 $
$ \therefore \triangle T M O $ 为等腰直角三角形
$ \therefore \angle T M O = 90 ^ { \circ } $,$ T M = O M $
$ \therefore \angle T M H + \angle O M N = 90 ^ { \circ } $
而 $ \angle O M N + \angle M O N = 90 ^ { \circ } $
$ \therefore \angle T M H = \angle M O N $
$ \because T H \perp B M $,$ \angle T H M = \angle M N O = 90 ^ { \circ } $
在 $ \triangle T H M $ 和 $ \triangle M N O $ 中
$ \because \angle T M H = \angle M O N $,$ \angle T H M = \angle M N O = 90 ^ { \circ } $
$ T M = O M $
$ \therefore \triangle T H M \cong \triangle M N O ( \mathrm { AAS } ) $
$ \therefore T H = M N $,$ \therefore H M = O N $
$ \because H K = H T $,$ \therefore H K = M N $
$ \therefore H K + K M = M N + K M $
$ \therefore K N = H M = O N $
$ \therefore \triangle K N O $ 为等腰直角三角形
$ \therefore \angle O K B = \angle K O N = 45 ^ { \circ } $
$ \therefore \angle O K B = 45 ^ { \circ } $
方法 2 (手拉手):过 M 作 $ M N \perp H B $ 交 TK 的延长线于 N,作 $ M G \perp O T $ 交 OT 于 G,连接 TM,OM
$ \because M ( - 2, - 2 ) $,$ \therefore \angle B O M = \angle T O M = 45 ^ { \circ } $
$ \therefore \triangle O G M $ 为等腰直角三角形
$ \therefore M G = O G = 2 $
又 $ \because T ( a, 0 ) $,$ a = - 4 $
$ \therefore O T = 4 $,$ \therefore M G = O G = T G = 2 $
$ \therefore \triangle T M O $ 为等腰直角三角形
$ \therefore \angle T M O = 90 ^ { \circ } $,$ T M = O M $
又 $ \because T H \perp O B $,$ H K = H T $
$ \therefore \triangle T H K $ 为等腰直角三角形
$ \therefore \angle H T K = \angle T K H = \angle M K N = 45 ^ { \circ } $
$ \because M N \perp H B $,$ \therefore \triangle K M N $ 为等腰直角三角形
$ \therefore M K = M N $,$ \angle M K N = \angle M N K = 45 ^ { \circ } $
$ \therefore \angle K M N + \angle T M K = \angle T M O + \angle T M K $
$ \therefore \angle O M K = \angle T M N $
在 $ \triangle O M K $ 和 $ \triangle T M N $ 中
$ \because O M = T M $ (已证),$ \angle O M K = \angle T M N $ (已证),$ K M = M N $ (已证),$ \therefore \triangle O M K \cong \triangle T M N ( \mathrm { SAS } ) $,$ \therefore \angle O K M = \angle T N M = 45 ^ { \circ } $,$ \therefore \angle O K B = 45 ^ { \circ } $
(1) $ \because M ( m, n ) $ 且 m,n 满足 $ m ^ { 2 } + 2 n ^ { 2 } - 2 m n + 4 n + 4 = 0 $
$ \therefore m ^ { 2 } - 2 m n + n ^ { 2 } + n ^ { 2 } + 4 n + 4 = 0 $
$ \therefore ( m - n ) ^ { 2 } + ( n + 2 ) ^ { 2 } = 0 $
$ \therefore m = n = - 2 $,$ \therefore $ 点 M 的坐标为 $ ( - 2, - 2 ) $
(2) 过 A 作 $ A E \perp x $ 轴于 D,交 OM 的延长线于 E
$ \therefore A E // O B $
$ \therefore \angle B O M = \angle A E M $,$ \angle O B M = \angle E A M $
在 $ \mathrm { Rt } \triangle A C B $ 中,$ \angle A C B = 90 ^ { \circ } $,$ \angle A B C = 45 ^ { \circ } $
$ \therefore \triangle A C B $ 为等腰直角三角形
$ \therefore A C = B C $
$ \because \angle A C D + \angle B C O = \angle B C O + \angle C B O = 90 ^ { \circ } $
$ \therefore \angle A C D = \angle C B O $
在 $ \mathrm { Rt } \triangle A D C $ 和 $ \mathrm { Rt } \triangle C O B $ 中
$ \because \angle A D C = \angle C O B = 90 ^ { \circ } $
$ A C = B C $,$ \angle A C D = \angle C B O $
$ \therefore \mathrm { Rt } \triangle A D C \cong \mathrm { Rt } \triangle C O B ( \mathrm { AAS } ) $
$ \therefore C D = B O $,$ A D = C O $
$ \because A ( a, t ) $,$ B ( 0, b ) $
$ \therefore D O = - a $,$ A D = C O = t $,$ C D = B O = - b $
$ \therefore D ( a, 0 ) $,$ C ( t, 0 ) $,$ C D = D O + C O = B O = - b $
$ \therefore t - a = - b $
$ \because M ( - 2, 2 ) $,$ \therefore \angle E O D = \angle B O E = 45 ^ { \circ } $
$ \therefore \triangle E D O $ 为等腰直角三角形
$ \therefore D O = D E = - a $
$ \therefore A E = A D + D E = t - a = - b = O B $
在 $ \triangle A E M $ 和 $ \triangle B O M $ 中
$ \because \angle B O M = \angle A E M $,$ A E = O B $,$ \angle O B M = \angle E A M $
$ \therefore \triangle A E M \cong \triangle B O M ( \mathrm { ASA } ) $
$ \therefore M E = M O $
$ \therefore D E = 2 \times 2 = 4 = D O $
$ \therefore a = - 4 $
(3) $ \angle O K B $ 的度数为 $ 45 ^ { \circ } $
方法 1 (三垂直):连接 TM,OM,作 $ O N \perp M B $,$ M G \perp O T $,垂足分别是 N,G
$ \therefore \angle O N M = \angle O G M = 90 ^ { \circ } $
$ \because M ( - 2, - 2 ) $
$ \therefore \angle B O M = \angle T O M = 45 ^ { \circ } $
$ \therefore \triangle O G M $ 为等腰直角三角形
$ \therefore M G = O G = 2 $
又 $ \because T ( a, 0 ) $,$ a = - 4 $
$ \therefore O T = 4 $,$ \therefore M G = O G = T G = 2 $
$ \therefore \triangle T M O $ 为等腰直角三角形
$ \therefore \angle T M O = 90 ^ { \circ } $,$ T M = O M $
$ \therefore \angle T M H + \angle O M N = 90 ^ { \circ } $
而 $ \angle O M N + \angle M O N = 90 ^ { \circ } $
$ \therefore \angle T M H = \angle M O N $
$ \because T H \perp B M $,$ \angle T H M = \angle M N O = 90 ^ { \circ } $
在 $ \triangle T H M $ 和 $ \triangle M N O $ 中
$ \because \angle T M H = \angle M O N $,$ \angle T H M = \angle M N O = 90 ^ { \circ } $
$ T M = O M $
$ \therefore \triangle T H M \cong \triangle M N O ( \mathrm { AAS } ) $
$ \therefore T H = M N $,$ \therefore H M = O N $
$ \because H K = H T $,$ \therefore H K = M N $
$ \therefore H K + K M = M N + K M $
$ \therefore K N = H M = O N $
$ \therefore \triangle K N O $ 为等腰直角三角形
$ \therefore \angle O K B = \angle K O N = 45 ^ { \circ } $
$ \therefore \angle O K B = 45 ^ { \circ } $
方法 2 (手拉手):过 M 作 $ M N \perp H B $ 交 TK 的延长线于 N,作 $ M G \perp O T $ 交 OT 于 G,连接 TM,OM
$ \because M ( - 2, - 2 ) $,$ \therefore \angle B O M = \angle T O M = 45 ^ { \circ } $
$ \therefore \triangle O G M $ 为等腰直角三角形
$ \therefore M G = O G = 2 $
又 $ \because T ( a, 0 ) $,$ a = - 4 $
$ \therefore O T = 4 $,$ \therefore M G = O G = T G = 2 $
$ \therefore \triangle T M O $ 为等腰直角三角形
$ \therefore \angle T M O = 90 ^ { \circ } $,$ T M = O M $
又 $ \because T H \perp O B $,$ H K = H T $
$ \therefore \triangle T H K $ 为等腰直角三角形
$ \therefore \angle H T K = \angle T K H = \angle M K N = 45 ^ { \circ } $
$ \because M N \perp H B $,$ \therefore \triangle K M N $ 为等腰直角三角形
$ \therefore M K = M N $,$ \angle M K N = \angle M N K = 45 ^ { \circ } $
$ \therefore \angle K M N + \angle T M K = \angle T M O + \angle T M K $
$ \therefore \angle O M K = \angle T M N $
在 $ \triangle O M K $ 和 $ \triangle T M N $ 中
$ \because O M = T M $ (已证),$ \angle O M K = \angle T M N $ (已证),$ K M = M N $ (已证),$ \therefore \triangle O M K \cong \triangle T M N ( \mathrm { SAS } ) $,$ \therefore \angle O K M = \angle T N M = 45 ^ { \circ } $,$ \therefore \angle O K B = 45 ^ { \circ } $
查看更多完整答案,请扫码查看


