18.(8分)如图,$C$是路段$AB$的中点,两人从$C$同时出发以相同的速度分别沿两条直线行走,并同时到达$D,E$两点.连接$AD,BE$,满足$DA⊥AB,EB⊥AB$,则$D,E$与路段$AB$的距离相等吗? 为什么?


答案:
由题意可知:CD=CE
∵C是AB的中点
∴CA=CB
∵DA⊥AB,EB⊥AB
∴∠A=∠B=90°
在Rt△DAC和Rt△EBC中
{CA=CB
CD=CE
∴Rt△DAC≌Rt△EBC(HL)
∴AD=BE
∵C是AB的中点
∴CA=CB
∵DA⊥AB,EB⊥AB
∴∠A=∠B=90°
在Rt△DAC和Rt△EBC中
{CA=CB
CD=CE
∴Rt△DAC≌Rt△EBC(HL)
∴AD=BE
19.(8分)如图所示,点$D,E$在$BC$上,$\triangle ABD\cong \triangle ACE$,求证:$\triangle ABE\cong \triangle ACD$.
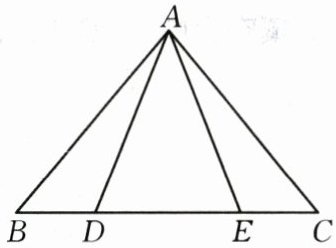

答案:
解:
因为$\triangle ABD\cong\triangle ACE$,
所以$AB = AC$,$BD = CE$,$\angle B=\angle C$。
由$BD = CE$可得$BD + DE=CE + DE$,即$BE = CD$。
在$\triangle ABE$和$\triangle ACD$中,
$\begin{cases}AB = AC\\\angle B=\angle C\\BE = CD\end{cases}$
根据$SAS$(边角边)定理,可得$\triangle ABE\cong\triangle ACD$。
因为$\triangle ABD\cong\triangle ACE$,
所以$AB = AC$,$BD = CE$,$\angle B=\angle C$。
由$BD = CE$可得$BD + DE=CE + DE$,即$BE = CD$。
在$\triangle ABE$和$\triangle ACD$中,
$\begin{cases}AB = AC\\\angle B=\angle C\\BE = CD\end{cases}$
根据$SAS$(边角边)定理,可得$\triangle ABE\cong\triangle ACD$。
20.(8分)如图,在$\triangle ABC$中,$∠C=90^{\circ },AD$是$∠BAC$的平分线,$DE⊥AB$于$E,F$在$AC$上,$BD=DF$,证明:
(1)$CF=EB$;
(2)$AB=AF+2EB$.
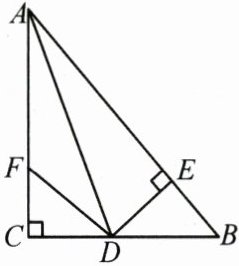
(1)$CF=EB$;
(2)$AB=AF+2EB$.

答案:
(1)
∵AD是∠BAC的平分线,
DE⊥AB,DC⊥AC,
∴DE=DC,
在Rt△CDF和Rt△EDB中,{DC=DE
DF=DB
∴Rt△CDF≌Rt△EDB(HL).
∴CF=EB;
(2)
∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,
∴CD=DE,
在Rt△ADC与Rt△ADE中,{DC=DE
AD=AD
∴Rt△ADC≌Rt△ADE(HL),
∴AC=AE,
∴AB=AE+BE=AC+EB=AF+CF+EB=AF+
2EB.
(1)
∵AD是∠BAC的平分线,
DE⊥AB,DC⊥AC,
∴DE=DC,
在Rt△CDF和Rt△EDB中,{DC=DE
DF=DB
∴Rt△CDF≌Rt△EDB(HL).
∴CF=EB;
(2)
∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,
∴CD=DE,
在Rt△ADC与Rt△ADE中,{DC=DE
AD=AD
∴Rt△ADC≌Rt△ADE(HL),
∴AC=AE,
∴AB=AE+BE=AC+EB=AF+CF+EB=AF+
2EB.
21.(8分)(1)如图1,$O$为$\triangle ABC$角平分线交点,作出点$C$;
(2)在图2中,①作$CE⊥AD$,交$AD$于点$E$;②在$AB$上画点$F$,使$∠ADC=∠BDF$;
(3)在图3中,找格点$F$,作$∠AFC=∠ABC$.
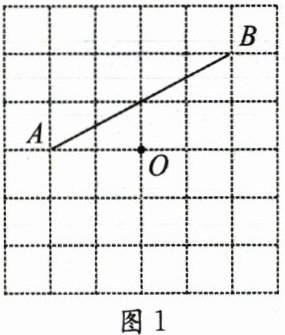


(2)在图2中,①作$CE⊥AD$,交$AD$于点$E$;②在$AB$上画点$F$,使$∠ADC=∠BDF$;
(3)在图3中,找格点$F$,作$∠AFC=∠ABC$.



答案:
本题为作图题,根据题目要求进行作图即可。
$(1)$ 作出点$C$
根据角平分线的性质,角平分线上的点到角两边的距离相等。已知$O$为$\triangle ABC$角平分线交点,延长$AO$、$BO$,根据格点的特点,确定$C$点位置(以$A$、$B$、$O$的相对位置关系,利用格点距离和角平分线性质确定$C$)。
$(2)$
① **作$CE\perp AD$,交$AD$于点$E$
利用直角三角板,使一条直角边与$AD$重合,另一条直角边过点$C$,沿过$C$点的直角边作直线,交$AD$于$E$,则$CE\perp AD$。
② **在$AB$上画点$F$,使$\angle ADC = \angle BDF$
以$D$为顶点,$DB$为一边,在$AB$上方作$\angle BDF=\angle ADC$,$DF$与$AB$的交点即为$F$点(可利用量角器或根据全等三角形、相似三角形等性质,结合格点构造相等角) 。
$(3)$ 找格点$F$,作$\angle AFC=\angle ABC$
根据圆周角定理:同弧所对的圆周角相等。以$AC$为弦,构造与$\angle ABC$相等的圆周角$\angle AFC$,通过格点确定$F$点位置(例如:找到$AC$的中垂线等方法,结合格点确定$F$使得$\angle AFC=\angle ABC$)。
由于这是作图题,需要借助直尺、三角板等工具按照上述思路在对应图形中完成作图。
综上,按照上述方法完成$\boldsymbol{(1)}$ $\boldsymbol{(2)}$ $\boldsymbol{(3)}$的**作图**。
$(1)$ 作出点$C$
根据角平分线的性质,角平分线上的点到角两边的距离相等。已知$O$为$\triangle ABC$角平分线交点,延长$AO$、$BO$,根据格点的特点,确定$C$点位置(以$A$、$B$、$O$的相对位置关系,利用格点距离和角平分线性质确定$C$)。
$(2)$
① **作$CE\perp AD$,交$AD$于点$E$
利用直角三角板,使一条直角边与$AD$重合,另一条直角边过点$C$,沿过$C$点的直角边作直线,交$AD$于$E$,则$CE\perp AD$。
② **在$AB$上画点$F$,使$\angle ADC = \angle BDF$
以$D$为顶点,$DB$为一边,在$AB$上方作$\angle BDF=\angle ADC$,$DF$与$AB$的交点即为$F$点(可利用量角器或根据全等三角形、相似三角形等性质,结合格点构造相等角) 。
$(3)$ 找格点$F$,作$\angle AFC=\angle ABC$
根据圆周角定理:同弧所对的圆周角相等。以$AC$为弦,构造与$\angle ABC$相等的圆周角$\angle AFC$,通过格点确定$F$点位置(例如:找到$AC$的中垂线等方法,结合格点确定$F$使得$\angle AFC=\angle ABC$)。
由于这是作图题,需要借助直尺、三角板等工具按照上述思路在对应图形中完成作图。
综上,按照上述方法完成$\boldsymbol{(1)}$ $\boldsymbol{(2)}$ $\boldsymbol{(3)}$的**作图**。
22.(10分)如图,在$\triangle ABC$中,$∠ACB=90^{\circ },AC=BC,BE⊥CE$于$E,AD⊥CE$于$D$.
(1) 求证:$∠BCE=∠CAD$;
(2) 若$AD=9\ \text{cm},DE=5\ \text{cm}$,求$BE$.
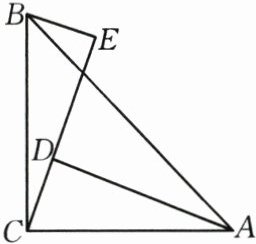
(1) 求证:$∠BCE=∠CAD$;
(2) 若$AD=9\ \text{cm},DE=5\ \text{cm}$,求$BE$.

答案:
证明:
(1)
∵BE⊥CE于E,AD⊥CE于D
∴∠ADC=∠CEB=90°
∵∠ACB=90°
∴∠BCE+∠ACD=90°
∵∠ACD+∠CAD=90°
∴∠BCE=∠CAD
(2)在△BCE和△CAD中
{∠BCE=∠CAD
∠BEC=∠CDA
BC=CA
∴△BCE≌△CAD(AAS)
∴AD=CE=9
∴BE=CD=9-5=4cm
(1)
∵BE⊥CE于E,AD⊥CE于D
∴∠ADC=∠CEB=90°
∵∠ACB=90°
∴∠BCE+∠ACD=90°
∵∠ACD+∠CAD=90°
∴∠BCE=∠CAD
(2)在△BCE和△CAD中
{∠BCE=∠CAD
∠BEC=∠CDA
BC=CA
∴△BCE≌△CAD(AAS)
∴AD=CE=9
∴BE=CD=9-5=4cm
查看更多完整答案,请扫码查看


