20. (8分)已知: ∠B=∠C=∠BAD, ∠ADC=∠DAC, AE⊥BC, 求∠DAE.


答案:
解:设$\angle B = \angle C = \angle BAD = x$。
在$\triangle ABC$中,根据三角形内角和定理$\angle BAC+\angle B+\angle C = 180^{\circ}$,$\angle BAC=\angle BAD+\angle DAC$,已知$\angle ADC = \angle DAC$。
又因为$\angle ADC=\angle B+\angle BAD$(三角形外角定理),所以$\angle ADC=\angle DAC = 2x$。
则$\angle BAC=x + 2x=3x$,那么$3x+x + x=180^{\circ}$,即$5x = 180^{\circ}$,解得$x = 36^{\circ}$。
所以$\angle DAC=2x = 72^{\circ}$。
因为$AE\perp BC$,在$\triangle AEC$中,$\angle AEC = 90^{\circ}$,$\angle C=x = 36^{\circ}$,根据三角形内角和定理$\angle EAC=180^{\circ}-\angle AEC-\angle C$,所以$\angle EAC=180^{\circ}-90^{\circ}-36^{\circ}=54^{\circ}$。
则$\angle DAE=\angle DAC-\angle EAC$,$\angle DAE=72^{\circ}-54^{\circ}=18^{\circ}$。
综上,$\angle DAE = 18^{\circ}$。
在$\triangle ABC$中,根据三角形内角和定理$\angle BAC+\angle B+\angle C = 180^{\circ}$,$\angle BAC=\angle BAD+\angle DAC$,已知$\angle ADC = \angle DAC$。
又因为$\angle ADC=\angle B+\angle BAD$(三角形外角定理),所以$\angle ADC=\angle DAC = 2x$。
则$\angle BAC=x + 2x=3x$,那么$3x+x + x=180^{\circ}$,即$5x = 180^{\circ}$,解得$x = 36^{\circ}$。
所以$\angle DAC=2x = 72^{\circ}$。
因为$AE\perp BC$,在$\triangle AEC$中,$\angle AEC = 90^{\circ}$,$\angle C=x = 36^{\circ}$,根据三角形内角和定理$\angle EAC=180^{\circ}-\angle AEC-\angle C$,所以$\angle EAC=180^{\circ}-90^{\circ}-36^{\circ}=54^{\circ}$。
则$\angle DAE=\angle DAC-\angle EAC$,$\angle DAE=72^{\circ}-54^{\circ}=18^{\circ}$。
综上,$\angle DAE = 18^{\circ}$。
21. (8分)如图, 已知AD//BC, AE, BE分别平分∠DAB, ∠CBA, 过E作FG分别交AD, BC于F, G, ∠AEF=28°, 求∠BEG的大小.


答案:
解:
因为$AD// BC$,所以$\angle DAB+\angle CBA = 180^{\circ}$。
因为$AE$,$BE$分别平分$\angle DAB$,$\angle CBA$,所以$\angle EAB=\frac{1}{2}\angle DAB$,$\angle EBA=\frac{1}{2}\angle CBA$。
则$\angle EAB+\angle EBA=\frac{1}{2}(\angle DAB+\angle CBA)=\frac{1}{2}×180^{\circ}=90^{\circ}$。
在$\triangle ABE$中,根据三角形内角和为$180^{\circ}$,可得$\angle AEB = 180^{\circ}-(\angle EAB+\angle EBA)=180^{\circ}-90^{\circ}=90^{\circ}$。
又因为$\angle AEF+\angle AEB+\angle BEG = 180^{\circ}$,$\angle AEF = 28^{\circ}$,所以$\angle BEG=180^{\circ}-\angle AEF-\angle AEB=180^{\circ}-28^{\circ}-90^{\circ}=62^{\circ}$。
综上,$\angle BEG$的大小为$62^{\circ}$。
因为$AD// BC$,所以$\angle DAB+\angle CBA = 180^{\circ}$。
因为$AE$,$BE$分别平分$\angle DAB$,$\angle CBA$,所以$\angle EAB=\frac{1}{2}\angle DAB$,$\angle EBA=\frac{1}{2}\angle CBA$。
则$\angle EAB+\angle EBA=\frac{1}{2}(\angle DAB+\angle CBA)=\frac{1}{2}×180^{\circ}=90^{\circ}$。
在$\triangle ABE$中,根据三角形内角和为$180^{\circ}$,可得$\angle AEB = 180^{\circ}-(\angle EAB+\angle EBA)=180^{\circ}-90^{\circ}=90^{\circ}$。
又因为$\angle AEF+\angle AEB+\angle BEG = 180^{\circ}$,$\angle AEF = 28^{\circ}$,所以$\angle BEG=180^{\circ}-\angle AEF-\angle AEB=180^{\circ}-28^{\circ}-90^{\circ}=62^{\circ}$。
综上,$\angle BEG$的大小为$62^{\circ}$。
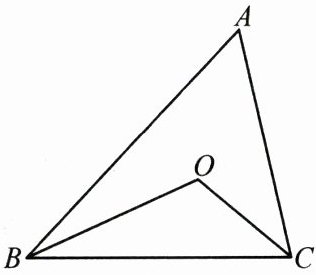
22. (10分)如图, 在△ABC中, BO, CO分别是∠ABC, ∠ACB的角平分线, 求:
(1)若∠A=50°, 求∠BOC的度数;
(2)在其他条件不变的情况下, ∠A与∠BOC之间有怎样的数量关系?
(1)若∠A=50°, 求∠BOC的度数;
(2)在其他条件不变的情况下, ∠A与∠BOC之间有怎样的数量关系?

答案:
22.
(1)$\because \angle A=50^{\circ }$,
$\therefore \angle ABC+\angle ACB=180^{\circ }-\angle A=130^{\circ }$,
$\because BO$,$CO$分别是$\triangle ABC$的角$\angle ABC$,$\angle ACB$的平分线,
$\therefore \angle OBC=\frac {1}{2}\angle ABC$,$\angle OCB=\frac {1}{2}\angle ACB$,
$\therefore \angle OBC+\angle OCB=\frac {1}{2}(\angle ABC+\angle ACB)=65^{\circ }$,
$\therefore \angle BOC=180^{\circ }-(\angle OBC+\angle OCB)=180^{\circ }-65^{\circ }=115^{\circ }$;
(2)$\because \angle ABC$与$\angle ACB$的平分线相交于点$O$,
$\therefore \angle OBC=\frac {1}{2}\angle ABC$,$\angle OCB=\frac {1}{2}\angle ACB$,
$\therefore \angle OBC+\angle OCB=\frac {1}{2}(\angle ABC+\angle ACB)$,
在$\triangle OBC$中,
$\angle BOC=180^{\circ }-(\angle OBC+\angle OCB)$
$=180^{\circ }-\frac {1}{2}(\angle ABC+\angle ACB)$
$=180^{\circ }-\frac {1}{2}(180^{\circ }-\angle A)$
$=90^{\circ }+\frac {1}{2}\angle A$,
即$\angle BOC=90^{\circ }+\frac {1}{2}\angle A$.
(1)$\because \angle A=50^{\circ }$,
$\therefore \angle ABC+\angle ACB=180^{\circ }-\angle A=130^{\circ }$,
$\because BO$,$CO$分别是$\triangle ABC$的角$\angle ABC$,$\angle ACB$的平分线,
$\therefore \angle OBC=\frac {1}{2}\angle ABC$,$\angle OCB=\frac {1}{2}\angle ACB$,
$\therefore \angle OBC+\angle OCB=\frac {1}{2}(\angle ABC+\angle ACB)=65^{\circ }$,
$\therefore \angle BOC=180^{\circ }-(\angle OBC+\angle OCB)=180^{\circ }-65^{\circ }=115^{\circ }$;
(2)$\because \angle ABC$与$\angle ACB$的平分线相交于点$O$,
$\therefore \angle OBC=\frac {1}{2}\angle ABC$,$\angle OCB=\frac {1}{2}\angle ACB$,
$\therefore \angle OBC+\angle OCB=\frac {1}{2}(\angle ABC+\angle ACB)$,
在$\triangle OBC$中,
$\angle BOC=180^{\circ }-(\angle OBC+\angle OCB)$
$=180^{\circ }-\frac {1}{2}(\angle ABC+\angle ACB)$
$=180^{\circ }-\frac {1}{2}(180^{\circ }-\angle A)$
$=90^{\circ }+\frac {1}{2}\angle A$,
即$\angle BOC=90^{\circ }+\frac {1}{2}\angle A$.
查看更多完整答案,请扫码查看


