9.根据下列已知条件,能唯一画出$\triangle ABC$的是(
A.$AB=2,BC=3,AC=6$
B.$AB=4,BC=3,∠A=50^{\circ }$
C.$∠A=50^{\circ },∠B=60^{\circ },AB=4$
D.$∠C=90^{\circ },AB=6$
C
)A.$AB=2,BC=3,AC=6$
B.$AB=4,BC=3,∠A=50^{\circ }$
C.$∠A=50^{\circ },∠B=60^{\circ },AB=4$
D.$∠C=90^{\circ },AB=6$
答案:
C
10.如图,$D$为$∠BAC$的外角平分线上一点并且满足$BD=CD,∠DBC=∠DCB$,过$D$作$DE⊥AC$于$E,DF⊥AB$交$BA$的延长线于$F$,则下列结论:
①$\triangle CDE\cong \triangle BDF$;②$CE=AB+AE$;③$∠BDC=∠BAC$;④$∠DAF=∠CBD$,其中正确的结论有(
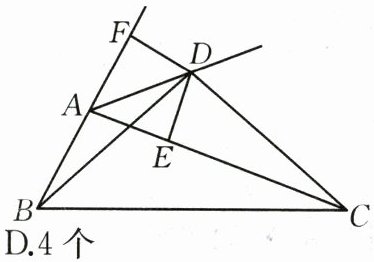
A.1个
B.2个
C.3个
D.4个
①$\triangle CDE\cong \triangle BDF$;②$CE=AB+AE$;③$∠BDC=∠BAC$;④$∠DAF=∠CBD$,其中正确的结论有(
D
)
A.1个
B.2个
C.3个
D.4个
答案:
D
11.如图所示,$AB=AC,AD=AE,∠BAC=∠DAE,∠1=35^{\circ },∠2=30^{\circ }$,则$∠3=$
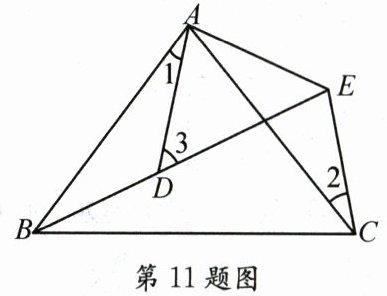
65°
.
答案:
65°
12.如图,在$\triangle ABC$中,$D,E$分别是边$AC,BC$上的点,若$\triangle ADB\cong \triangle EDB\cong \triangle EDC$,则$∠C=$
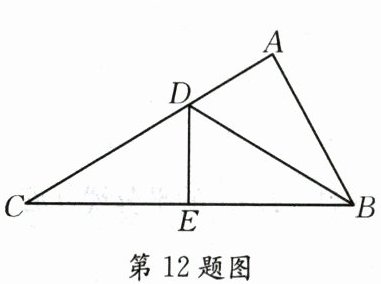
30°
.
答案:
30°
13.如图,$AB=AC,∠BAC=90^{\circ },BM⊥AD$于$M,CN⊥AD$于$N,CN+AN=8\ \text{cm},MN=4\ \text{cm}$,则$AM$的长为____

6cm
.
答案:
6cm
14.如图,$\triangle ABO$的边$OB$在$x$轴上,$∠A=2∠ABO,OC$平分$∠AOB$交$AB$于点$C$,若$AC=2,OA=3$,则点$B$的坐标为

(5,0)
.
答案:
(5,0)
15.如图,$A(1,0),B(0,2)$,在$y$轴左侧有一点$C$,使$\triangle BOC$与$\triangle BOA$全等,则点$C$的坐标为
(-1,2)或(-1,0)
.
答案:
(-1,2)或(-1,0)
16.如图,$AD// BC,∠DAB=∠ABC=90^{\circ }$,将$CD$绕$D$逆时针旋转$90^{\circ }$至$DE$,连接$AE$,若$AD=3,BC=5$,则$\triangle ADE$的面积是____
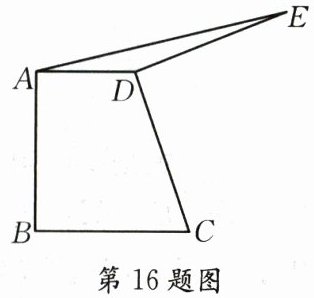
3
.
答案:
3
17.(8分)如图,已知$AC$与$BD$交于点$O,OA=OC,OB=OD$,求证:$AB=CD$.
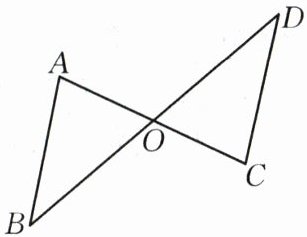

答案:
【解析】:
在$\triangle AOB$和$\triangle COD$中,
$\begin{cases}OA = OC\\\angle AOB=\angle COD\\OB = OD\end{cases}$(对顶角相等)
根据“边角边”($SAS$)判定定理,可得$\triangle AOB\cong\triangle COD$。
因为全等三角形的对应边相等,所以$AB = CD$。
【答案】:
在$\triangle AOB$和$\triangle COD$中,$\begin{cases}OA = OC\\\angle AOB=\angle COD\\OB = OD\end{cases}$,所以$\triangle AOB\cong\triangle COD(SAS)$,则$AB = CD$。
在$\triangle AOB$和$\triangle COD$中,
$\begin{cases}OA = OC\\\angle AOB=\angle COD\\OB = OD\end{cases}$(对顶角相等)
根据“边角边”($SAS$)判定定理,可得$\triangle AOB\cong\triangle COD$。
因为全等三角形的对应边相等,所以$AB = CD$。
【答案】:
在$\triangle AOB$和$\triangle COD$中,$\begin{cases}OA = OC\\\angle AOB=\angle COD\\OB = OD\end{cases}$,所以$\triangle AOB\cong\triangle COD(SAS)$,则$AB = CD$。
查看更多完整答案,请扫码查看


