1. (2024·徐州中考)古汉字“雷”的下列四种写法,可以看作轴对称图形的是 (

D
)
答案:
D
2. 等腰三角形的一个内角为70°,则另外两个内角的度数分别是 (
A.55°,55°
B.70°,40°或70°,55°
C.70°,40°
D.55°,55°或70°,40°
D
)A.55°,55°
B.70°,40°或70°,55°
C.70°,40°
D.55°,55°或70°,40°
答案:
解:
情况一:70°为顶角
底角 = (180° - 70°) ÷ 2 = 55°
另外两个内角为55°,55°
情况二:70°为底角
顶角 = 180° - 70°×2 = 40°
另外两个内角为70°,40°
综上,另外两个内角的度数分别是55°,55°或70°,40°。
答案:D
情况一:70°为顶角
底角 = (180° - 70°) ÷ 2 = 55°
另外两个内角为55°,55°
情况二:70°为底角
顶角 = 180° - 70°×2 = 40°
另外两个内角为70°,40°
综上,另外两个内角的度数分别是55°,55°或70°,40°。
答案:D
3. 将平面直角坐标系内的△ABC的三个顶点坐标的横坐标乘-1,纵坐标不变,则所得的三角形与原三角形 (
A.关于x轴对称
B.关于y轴对称
C.关于直线y= x对称
D.无任何对称关系
B
)A.关于x轴对称
B.关于y轴对称
C.关于直线y= x对称
D.无任何对称关系
答案:
解:在平面直角坐标系中,点$(x,y)$关于$y$轴对称的点的坐标为$(-x,y)$。
将$\triangle ABC$三个顶点坐标的横坐标乘$-1$,纵坐标不变,即每个顶点$(x,y)$变为$(-x,y)$,符合关于$y$轴对称的坐标特征。
因此,所得三角形与原三角形关于$y$轴对称。
答案:B
将$\triangle ABC$三个顶点坐标的横坐标乘$-1$,纵坐标不变,即每个顶点$(x,y)$变为$(-x,y)$,符合关于$y$轴对称的坐标特征。
因此,所得三角形与原三角形关于$y$轴对称。
答案:B
4. 一个三角形任意一边上的高都是这边上的中线,则对这个三角形的形状最准确的判断是 (
A.等腰三角形
B.直角三角形
C.等边三角形
D.等腰直角三角形
C
)A.等腰三角形
B.直角三角形
C.等边三角形
D.等腰直角三角形
答案:
解:设三角形为△ABC,AD是BC边上的高且为中线。
∵AD是BC边上的中线,
∴BD=DC。
∵AD是BC边上的高,
∴∠ADB=∠ADC=90°。
在△ADB和△ADC中,AD=AD,∠ADB=∠ADC,BD=DC,
∴△ADB≌△ADC(SAS),
∴AB=AC。
同理可证AB=BC,AC=BC。
∴AB=BC=AC,△ABC是等边三角形。
答案:C
∵AD是BC边上的中线,
∴BD=DC。
∵AD是BC边上的高,
∴∠ADB=∠ADC=90°。
在△ADB和△ADC中,AD=AD,∠ADB=∠ADC,BD=DC,
∴△ADB≌△ADC(SAS),
∴AB=AC。
同理可证AB=BC,AC=BC。
∴AB=BC=AC,△ABC是等边三角形。
答案:C
5. 等腰三角形的两个外角的度数比为2:5,则它的顶角的度数是 (
A.40°
B.120°
C.140°
D.40°或140°
B
)A.40°
B.120°
C.140°
D.40°或140°
答案:
解:设等腰三角形的底角为$x$,顶角为$y$,则$2x + y = 180^\circ$。
情况1:两个外角均为底角的外角
底角的外角为$180^\circ - x$,则外角比为$1:1$,不符合$2:5$,舍去。
情况2:一个外角为底角的外角,一个为顶角的外角
底角外角:$180^\circ - x$,顶角外角:$180^\circ - y$。
分两种子情况:
- 若$(180^\circ - x):(180^\circ - y) = 2:5$,则$5(180^\circ - x) = 2(180^\circ - y)$。
联立$2x + y = 180^\circ$,解得$x = 100^\circ$,此时两底角和$200^\circ > 180^\circ$,舍去。
- 若$(180^\circ - x):(180^\circ - y) = 5:2$,则$2(180^\circ - x) = 5(180^\circ - y)$。
联立$2x + y = 180^\circ$,解得$y = 120^\circ$,符合题意。
结论:顶角的度数是$120^\circ$。
答案:B
情况1:两个外角均为底角的外角
底角的外角为$180^\circ - x$,则外角比为$1:1$,不符合$2:5$,舍去。
情况2:一个外角为底角的外角,一个为顶角的外角
底角外角:$180^\circ - x$,顶角外角:$180^\circ - y$。
分两种子情况:
- 若$(180^\circ - x):(180^\circ - y) = 2:5$,则$5(180^\circ - x) = 2(180^\circ - y)$。
联立$2x + y = 180^\circ$,解得$x = 100^\circ$,此时两底角和$200^\circ > 180^\circ$,舍去。
- 若$(180^\circ - x):(180^\circ - y) = 5:2$,则$2(180^\circ - x) = 5(180^\circ - y)$。
联立$2x + y = 180^\circ$,解得$y = 120^\circ$,符合题意。
结论:顶角的度数是$120^\circ$。
答案:B
6. (2024秋·南通海门区校级期中)如图,在△ABC中,∠B= 76°,边AC的垂直平分线交BC于点D,交AC于点E,连接AD,若AB+BD= BC,则∠C的度数为 (
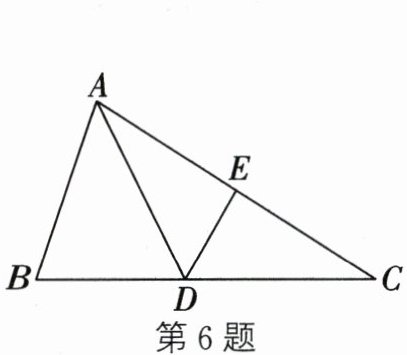
A.28°
B.38°
C.36°
D.30°
B
)
A.28°
B.38°
C.36°
D.30°
答案:
解:
∵DE是AC的垂直平分线,
∴AD=CD,
∴∠C=∠CAD。
设∠C=∠CAD=x,则∠ADB=∠C+∠CAD=2x。
∵AB+BD=BC,BC=BD+CD,
∴AB=CD,
∵AD=CD,
∴AB=AD,
∴∠ADB=∠B=76°,
即2x=76°,
解得x=38°,
∴∠C=38°。
答案:B
∵DE是AC的垂直平分线,
∴AD=CD,
∴∠C=∠CAD。
设∠C=∠CAD=x,则∠ADB=∠C+∠CAD=2x。
∵AB+BD=BC,BC=BD+CD,
∴AB=CD,
∵AD=CD,
∴AB=AD,
∴∠ADB=∠B=76°,
即2x=76°,
解得x=38°,
∴∠C=38°。
答案:B
7. 如图,在△ABC中,D、E分别是BC、AC的中点,DE//AB,BF平分∠ABC,交DE于点F.若BC= 8,则DF的长是 (
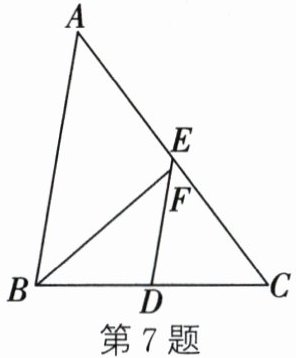
A.2
B.3
C.2.5
D.4
D
)
A.2
B.3
C.2.5
D.4
答案:
解:
∵D、E分别是BC、AC的中点,
∴DE是△ABC的中位线,
∴DE//AB,且DE = $\frac{1}{2}$AB,BD = $\frac{1}{2}$BC = 4。
∵DE//AB,
∴∠ABF = ∠DFB。
∵BF平分∠ABC,
∴∠ABF = ∠DBF。
∴∠DFB = ∠DBF,
∴DF = BD = 4。
答案:D
∵D、E分别是BC、AC的中点,
∴DE是△ABC的中位线,
∴DE//AB,且DE = $\frac{1}{2}$AB,BD = $\frac{1}{2}$BC = 4。
∵DE//AB,
∴∠ABF = ∠DFB。
∵BF平分∠ABC,
∴∠ABF = ∠DBF。
∴∠DFB = ∠DBF,
∴DF = BD = 4。
答案:D
8. 在△ABC中,AB= AC,BC= 10,AB的垂直平分线与AC的垂直平分线分别交BC于点D、E,且DE= 4,则AD+AE的值为 (
A.6
B.10
C.6或14
D.6或10
C
)A.6
B.10
C.6或14
D.6或10
答案:
解:
∵AB=AC,
∴△ABC是等腰三角形。
∵AB的垂直平分线交BC于D,
∴AD=BD。
∵AC的垂直平分线交BC于E,
∴AE=CE。
情况1:D在E左侧
∵BC=10,DE=4,
∴AD+AE=BD+CE=BC-DE=10-4=6。
情况2:D在E右侧
∵BC=10,DE=4,
∴AD+AE=BD+CE=BC+DE=10+4=14。
综上,AD+AE的值为6或14。
答案:C
∵AB=AC,
∴△ABC是等腰三角形。
∵AB的垂直平分线交BC于D,
∴AD=BD。
∵AC的垂直平分线交BC于E,
∴AE=CE。
情况1:D在E左侧
∵BC=10,DE=4,
∴AD+AE=BD+CE=BC-DE=10-4=6。
情况2:D在E右侧
∵BC=10,DE=4,
∴AD+AE=BD+CE=BC+DE=10+4=14。
综上,AD+AE的值为6或14。
答案:C
9. 如图,E是等边△ABC中AC边上的点,∠1= ∠2,BE= CD,则△ADE的形状是 (
A.等腰三角形
B.等边三角形
C.不等边三角形
D.不能确定形状
B
)A.等腰三角形
B.等边三角形
C.不等边三角形
D.不能确定形状
答案:
解:
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°。
在△ABE和△ACD中,
AB=AC,
∠1=∠2,
BE=CD,
∴△ABE≌△ACD(SAS)。
∴AE=AD,∠BAE=∠CAD=60°。
∴△ADE是等边三角形。
答案:B
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°。
在△ABE和△ACD中,
AB=AC,
∠1=∠2,
BE=CD,
∴△ABE≌△ACD(SAS)。
∴AE=AD,∠BAE=∠CAD=60°。
∴△ADE是等边三角形。
答案:B
查看更多完整答案,请扫码查看


