《2025年轻松作业本八年级数学上册人教版》

1. (2024 春·海安期末)若一个三角形的两边长分别为 2 cm 和 4 cm,则第三边的长可能是(C)
A.1 cm
B.2 cm
C.4 cm
D.6 cm

答案： 设第三边的长为$x$cm。
根据三角形三边关系：两边之和大于第三边，两边之差小于第三边。
可得：$4 - 2 ＜ x ＜ 4 + 2$，即$2 ＜ x ＜ 6$。
选项中只有$4$cm 满足条件。
答案：C

2. (2024·武汉中考)现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性. 下列汉字是轴对称图形的是(C)

答案： C

3. 下列四组条件中,可以判定△ABC 与$△A_1B_1C_1 $全等的是(C)
$A. BC = B_1C_1,AC = A_1C_1,∠A = ∠A_1$

$B. AB = A_1B_1,∠C = ∠C_1 = 90°$

$C. AC = A_1C_1,∠A = ∠A_1,∠B = ∠B_1$

$D. ∠A = ∠A_1,∠B = ∠B_1,∠C = ∠C_1$

答案： 解：选项A：已知两边及其中一边的对角对应相等（SSA），不能判定全等。
选项B：仅有一组直角边和直角对应相等（HL条件不完整），不能判定全等。
选项C：两角及夹边对应相等（ASA），可以判定全等。
选项D：三组角对应相等（AAA），只能判定相似，不能判定全等。
结论：C

4. 如图,点 E、F 在线段 BC 上,△ABF 与△DEC 全等,点 A 和点 D,点 B 和点 C 是对应点,AF 和 DE 交于点 M,则与 EM 相等的线段是(D)
A.BE
B.EF
C.FC
D.MF

答案： 解：
∵△ABF≌△DCE，点A和点D，点B和点C是对应点，
∴AF=DE，∠AFB=∠DEC．
在△MEF中，∠AFB=∠DEC，
∴MF=EM．
答案：D

5. 如图,直线 m // n,△ABC 是等边三角形,顶点 B 在直线 n 上,直线 m 交 AB 于点 E,交 AC 于点 F,若∠1 = 140°,则∠2 的度数是(B)
A.80°
B.100°
C.120°
D.140°

答案： 解：
∵△ABC是等边三角形，
∴∠A=60°，∠ABC=60°。
∵∠1=140°，∠1+∠AFE=180°，
∴∠AFE=180°-140°=40°。
在△AEF中，∠AEF=180°-∠A-∠AFE=180°-60°-40°=80°。
∵m//n，
∴∠AEF=∠ABE=80°。
∵∠ABE+∠2=180°，
∴∠2=180°-80°=100°。
答案：B

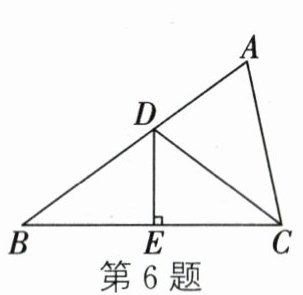
6. 如图,DE 是△ABC 的边 BC 的垂直平分线,分别交边 AB、BC 于点 D、E,且 AB = 9,AC = 6,则△ACD 的周长是(C)

A.10.5
B.12
C.15
D.18

答案：
∵DE是△ABC的边BC的垂直平分线，
∴DB=DC。
∵AB=9，AC=6，
∴△ACD的周长=AD+DC+AC=AD+DB+AC=AB+AC=9+6=15。
答案：C

7. 如图,AO、BO 分别平分∠CAB、∠CBA,且点 O 到 AB 的距离 OD = 2,△ABC 的周长为 28,则△ABC 的面积为(D)
A.7
B.14
C.21
D.28

答案： 1. 首先，根据角平分线的性质：
因为$AO$平分$\angle CAB$，$BO$平分$\angle CBA$，点$O$到$AB$的距离$OD = 2$，根据角平分线的性质“角平分线上的点到角两边的距离相等”，所以点$O$到$AC$的距离等于$OD$，点$O$到$BC$的距离也等于$OD$。
2. 然后，计算$\triangle ABC$的面积：
设点$O$到$AC$的距离为$h_1$，点$O$到$BC$的距离为$h_2$，则$h_1 = h_2=OD = 2$。
根据三角形面积公式$S=\frac{1}{2}ah$（$a$为底，$h$为高），$S_{\triangle ABC}=S_{\triangle AOC}+S_{\triangle AOB}+S_{\triangle BOC}$。
$S_{\triangle AOC}=\frac{1}{2}AC\cdot h_1$，$S_{\triangle AOB}=\frac{1}{2}AB\cdot OD$，$S_{\triangle BOC}=\frac{1}{2}BC\cdot h_2$。
因为$h_1 = h_2 = OD = 2$，所以$S_{\triangle ABC}=\frac{1}{2}(AC + AB+BC)\cdot OD$。
已知$\triangle ABC$的周长$AC + AB + BC=28$，$OD = 2$。
把$AC + AB + BC = 28$，$OD = 2$代入$S_{\triangle ABC}=\frac{1}{2}(AC + AB + BC)\cdot OD$中，可得$S_{\triangle ABC}=\frac{1}{2}×28×2$。
计算$\frac{1}{2}×28×2=28$。
所以$\triangle ABC$的面积为$28$，答案是D。

8. (2024·邢台三模)将等腰直角三角板 ABC 按如图的方式放置,点 A 在 x 轴的正半轴上移动,点 B 随之在 y 轴的正半轴上移动,点 C 在 AB 的左侧,设点 C 的横坐标为 n,则它的纵坐标为(B)
A.n
B.-n
C.√2n
D.-√2n

答案： 解：过点C作CD⊥x轴于D，CE⊥y轴于E，
则四边形CDOE是矩形，
∴CE=OD=-n，CD=OE。
∵△ABC是等腰直角三角形，
∴AC=BC，∠ACB=90°。
∵∠BCE+∠ECA=90°，∠ECA+∠ACD=90°，
∴∠BCE=∠ACD。
在△BCE和△ACD中，
∠BEC=∠ADC=90°，∠BCE=∠ACD，BC=AC，
∴△BCE≌△ACD(AAS)，
∴BE=AD，CE=CD。
∵CE=-n，
∴CD=-n，即点C的纵坐标为-n。
答案：B