《2025年轻松作业本八年级数学上册人教版》

20. (5分)如图,在$\triangle ABC$中,$AB = 3$,$AC = 5$.
(1)直接写出BC长的取值范围是$2 ＜ BC ＜ 8$；
(2)若D是BC边上的一点,$\angle BAC = 85^{\circ}$,$\angle ADC = 140^{\circ}$,$\angle BAD = \angle B$,求$\angle C$的度数.

解：$∵∠ADC$是$\triangle ABD$的外角
$∴∠ADC = ∠B + ∠BAD = 140^{\circ}$
$∵∠B = ∠BAD$
$∴∠B = \frac{1}{2}×140^{\circ} = 70^{\circ}$
$∵∠B + ∠BAC + ∠C = 180^{\circ}$
$∴∠C = 180^{\circ} - ∠B - ∠BAC$
$= 180^{\circ} - 70^{\circ} - 85^{\circ}$
$= 25^{\circ}$

答案：
(1) $2 ＜ BC ＜ 8$
(2) 解：$∵∠ADC$是$\triangle ABD$的外角
$∴∠ADC = ∠B + ∠BAD = 140^{\circ}$
$∵∠B = ∠BAD$
$∴∠B = \frac{1}{2}×140^{\circ} = 70^{\circ}$
$∵∠B + ∠BAC + ∠C = 180^{\circ}$
$∴∠C = 180^{\circ} - ∠B - ∠BAC$
$= 180^{\circ} - 70^{\circ} - 85^{\circ}$
$= 25^{\circ}$

21. (5分)如图,在$\triangle ABC$中,AD平分$\angle BAC$,点P为线段AD上的一点,过点P作$PE\perp AD$,交BC的延长线于点E.若$\angle B = 35^{\circ}$,$\angle E = 25^{\circ}$,求$\angle ACB$的度数.

答案： 解：$∵PE⊥AD$，
$∴∠DPE=90^{\circ}$。
$∵∠DPE+∠PDE+∠E=180^{\circ}$，
$∴∠PDE=180^{\circ}-∠DPE-∠E=180^{\circ}-90^{\circ}-25^{\circ}=65^{\circ}$。
$∵∠PDE$是$△ABD$的外角，
$∴∠PDE=∠B+∠BAD$。
$∵∠B=35^{\circ}$，
$∴∠BAD=∠PDE-∠B=65^{\circ}-35^{\circ}=30^{\circ}$。
$∵AD$平分$∠BAC$，
$∴∠BAC=2∠BAD=2×30^{\circ}=60^{\circ}$。
$∵$在$△ABC$中，$∠BAC+∠B+∠ACB=180^{\circ}$，
$∴∠ACB=180^{\circ}-∠BAC-∠B=180^{\circ}-60^{\circ}-35^{\circ}=85^{\circ}$。

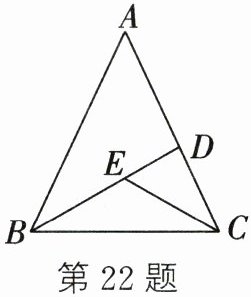
22. (5分)(2024春·南通崇川区校级月考)如图,$\angle A = 65^{\circ}$,$\angle ABD = 30^{\circ}$,$\angle ACB = 72^{\circ}$,且CE平分$\angle ACB$,求$\angle BEC$的度数.

答案： 1. 首先，在$\triangle ABC$中，根据三角形内角和定理$\angle A+\angle ABC+\angle ACB = 180^{\circ}$：
已知$\angle A = 65^{\circ}$，$\angle ACB = 72^{\circ}$，则$\angle ABC=180^{\circ}-\angle A - \angle ACB$。
把$\angle A = 65^{\circ}$，$\angle ACB = 72^{\circ}$代入可得：$\angle ABC=180 - 65-72=43^{\circ}$。
又因为$\angle ABD = 30^{\circ}$，所以$\angle DBC=\angle ABC-\angle ABD$。
把$\angle ABC = 43^{\circ}$，$\angle ABD = 30^{\circ}$代入得：$\angle DBC=43 - 30 = 13^{\circ}$。
2. 然后，因为$CE$平分$\angle ACB$：
根据角平分线定义，$\angle ECB=\frac{1}{2}\angle ACB$。
已知$\angle ACB = 72^{\circ}$，所以$\angle ECB=\frac{1}{2}×72^{\circ}=36^{\circ}$。
3. 最后，在$\triangle BEC$中，根据三角形内角和定理$\angle BEC+\angle EBC+\angle ECB = 180^{\circ}$：
则$\angle BEC=180^{\circ}-\angle EBC-\angle ECB$。
把$\angle EBC = 13^{\circ}$，$\angle ECB = 36^{\circ}$代入可得：$\angle BEC=180 - 13-36=131^{\circ}$。
所以$\angle BEC$的度数为$131^{\circ}$。

23. (12分)(2024·平顶山期末)如图,点C、D分别在射线OA、OB上,CE是$\angle ACD$的平分线,CE的反向延长线与$\angle ODC$的平分线交于点P.
(1)如图①,当$\angle AOB = \angle OCD = 60^{\circ}$时,$\angle P = $$30^{\circ}$；
(2)如图②,当$\angle AOB = 60^{\circ}$,点C、D在射线OA、OB上任意移动时(不与点O重合),$\angle P$的大小是否变化？若变化,请说明理由；若不变化,请求出$\angle P$的度数；
$\angle P$的大小不变，$\angle P = 30^{\circ}$
证明：$\because CE$平分$\angle ACD$，$DP$平分$\angle ODC$
$\therefore \angle ECD=\frac{1}{2}\angle ACD$，$\angle PDC=\frac{1}{2}\angle ODC$
$\because \angle ECD = \angle P+\angle PDC$
$\therefore \frac{1}{2}\angle ACD=\angle P+\frac{1}{2}\angle ODC$
$\because \angle ACD=\angle AOB+\angle ODC$
$\therefore \frac{1}{2}(\angle AOB+\angle ODC)=\angle P+\frac{1}{2}\angle ODC$
$\therefore \frac{1}{2}\angle AOB+\frac{1}{2}\angle ODC=\angle P+\frac{1}{2}\angle ODC$
$\therefore \angle P=\frac{1}{2}\angle AOB$
$\because \angle AOB = 60^{\circ}$
$\therefore \angle P=\frac{1}{2}×60^{\circ}=30^{\circ}$
(3)如图③,若$\angle OCD+\angle ODC = \alpha(0^{\circ}＜\alpha＜180^{\circ})$,请直接写出$\angle P$的度数(用含$\alpha$的式子表示).
$90^{\circ}-\frac{1}{2}\alpha$

答案：
(1) $30^{\circ}$
(2) $\angle P$的大小不变，$\angle P = 30^{\circ}$
证明：$\because CE$平分$\angle ACD$，$DP$平分$\angle ODC$
$\therefore \angle ECD=\frac{1}{2}\angle ACD$，$\angle PDC=\frac{1}{2}\angle ODC$
$\because \angle ECD = \angle P+\angle PDC$
$\therefore \frac{1}{2}\angle ACD=\angle P+\frac{1}{2}\angle ODC$
$\because \angle ACD=\angle AOB+\angle ODC$
$\therefore \frac{1}{2}(\angle AOB+\angle ODC)=\angle P+\frac{1}{2}\angle ODC$
$\therefore \frac{1}{2}\angle AOB+\frac{1}{2}\angle ODC=\angle P+\frac{1}{2}\angle ODC$
$\therefore \angle P=\frac{1}{2}\angle AOB$
$\because \angle AOB = 60^{\circ}$
$\therefore \angle P=\frac{1}{2}×60^{\circ}=30^{\circ}$
(3) $90^{\circ}-\frac{1}{2}\alpha$