《2025年轻松作业本八年级数学上册人教版》

16. 如图,$BD是\triangle ABC的外角\angle ABP$的平分线,$DA= DC$,$DE\perp BP于点E$.若$AB= 5$,$BC= 3$,则$BE$的长为______1.

答案： 1. 首先，过点$D$作$DF\perp AB$于点$F$：
因为$BD$是$\angle ABP$的平分线，$DE\perp BP$，$DF\perp AB$，根据角平分线的性质：角平分线上的点到角两边的距离相等，所以$DE = DF$。
在$Rt\triangle ADF$和$Rt\triangle CDE$中，$\left\{\begin{array}{l}DA = DC\\DF = DE\end{array}\right.$。
根据$HL$（斜边 - 直角边）定理，可得$Rt\triangle ADF\cong Rt\triangle CDE$，所以$AF = CE$。
2. 然后，在$Rt\triangle BDE$和$Rt\triangle BDF$中：
因为$\left\{\begin{array}{l}DE = DF\\BD = BD\end{array}\right.$，根据$HL$定理，$Rt\triangle BDE\cong Rt\triangle BDF$，所以$BE = BF$。
3. 接着，设$BE=x$：
则$BF = x$，$AF=AB - BF=5 - x$，$CE = BC + BE=3 + x$。
又因为$AF = CE$，所以$5−x = 3 + x$。
4. 最后，解方程：
移项可得：$-x - x=3 - 5$，即$-2x=-2$。
两边同时除以$-2$，得$x = 1$。
故$BE$的长为$1$。

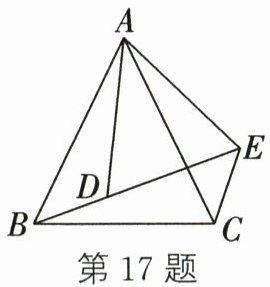
17. (2024·重庆潼南区一模)如图,已知$AB= AC$,$AD= AE$,$\angle BAC= \angle DAE= 52^{\circ}$,$B$、$D$、$E$在同一直线上,则$\angle BEC$的度数为______.

52°

答案： 解：
∵∠BAC=∠DAE=52°，
∴∠BAC-∠DAC=∠DAE-∠DAC，即∠BAD=∠CAE．
在△ABD和△ACE中，
∵AB=AC，∠BAD=∠CAE，AD=AE，
∴△ABD≌△ACE（SAS）．
∴∠ABD=∠ACE．
设AC与BE交于点O，
∵∠AOB=∠COE，
∴∠BEC=∠BAC=52°．
52°

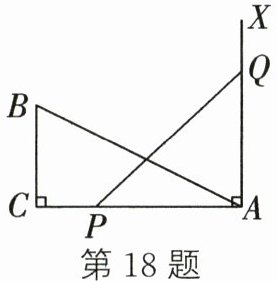
18. 如图,在$Rt\triangle ABC$中,$\angle ACB= 90^{\circ}$,$AC= 10cm$,$BC= 5cm$,$PQ= AB$,$P$、$Q两点分别在AC和AC的垂线AX$上移动.当$AP$的长为$5cm$或$10cm$时,$\triangle ABC和\triangle APQ$全等.

答案： 解：在$Rt\triangle ABC$和$Rt\triangle APQ$中，$\angle ACB = \angle PAQ = 90^{\circ}$，$PQ = AB$。
情况一：当$AP = BC$时，
$AP = BC = 5cm$，
在$Rt\triangle ABC$和$Rt\triangle QPA$中，
$\left\{\begin{array}{l} AP = BC \\ PQ = AB \end{array}\right.$，
$\therefore Rt\triangle ABC \cong Rt\triangle QPA(HL)$。
情况二：当$AP = AC$时，
$AP = AC = 10cm$，
在$Rt\triangle ABC$和$Rt\triangle PQA$中，
$\left\{\begin{array}{l} AP = AC \\ PQ = AB \end{array}\right.$，
$\therefore Rt\triangle ABC \cong Rt\triangle PQA(HL)$。
综上，$AP$的长为$5cm$或$10cm$。
答案：$5cm$或$10cm$

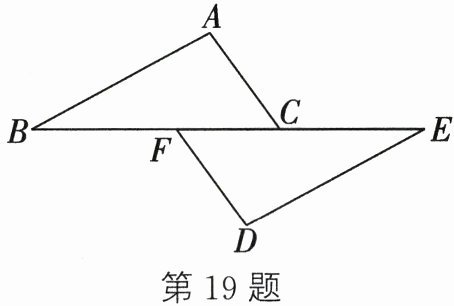
19. (6分)(2024秋·如皋期末)如图,点$B$、$F$、$C$、$E$在同一条直线上,$AB= DE$,$AB// DE$,$AC// DF$.
(1) 求证:$\triangle ABC\cong \triangle DEF$;
(2) 若$BE= 8$,$FC= 2$,求$BF$的长.

答案： （1）证明：$\because AB// DE$，$AC// DF$，
$\therefore \angle B=\angle E$，$\angle ACB=\angle DFE$。
在$\triangle ABC$和$\triangle DEF$中，
$\left\{\begin{array}{l} \angle B=\angle E,\\ \angle ACB=\angle DFE,\\ AB=DE,\end{array}\right.$
$\therefore \triangle ABC\cong \triangle DEF(AAS)$。
（2）解：$\because \triangle ABC\cong \triangle DEF$，
$\therefore BC=EF$。
$\because BC=BF+FC$，$EF=FC+EC$，
$\therefore BF+FC=FC+EC$，
$\therefore BF=EC$。
$\because BE=BF+FC+EC$，$BF=EC$，
$\therefore BE=2BF+FC$。
$\because BE=8$，$FC=2$，
$\therefore 8=2BF+2$，
解得$BF=3$。

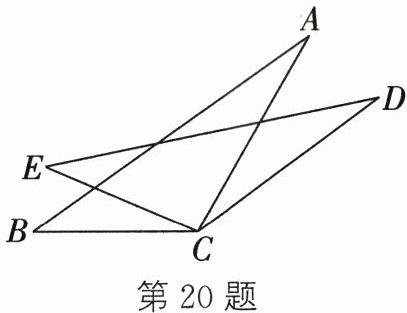
20. (10分)(2024·启东一模)如图,$CA= CD$,$\angle BCE= \angle ACD$,$BC= EC$.
(1) 求证:$AB= DE$;
(2) 若$\angle A= 25^{\circ}$,$\angle E= 35^{\circ}$,求$\angle ECD$的度数.

答案： （1）证明：$\because \angle BCE = \angle ACD$，
$\therefore \angle BCE + \angle ACE = \angle ACD + \angle ACE$，即$\angle ACB = \angle DCE$。
在$\triangle ACB$和$\triangle DCE$中，
$\left\{\begin{array}{l} CA = CD,\\ \angle ACB = \angle DCE,\\ BC = EC,\end{array}\right.$
$\therefore \triangle ACB \cong \triangle DCE(SAS)$，
$\therefore AB = DE$。
（2）解：由（1）得$\triangle ACB \cong \triangle DCE$，
$\therefore \angle A = \angle D = 25^{\circ}$。
$\because \angle E = 35^{\circ}$，
$\therefore \angle ECD = 180^{\circ} - \angle D - \angle E = 180^{\circ} - 25^{\circ} - 35^{\circ} = 120^{\circ}$。

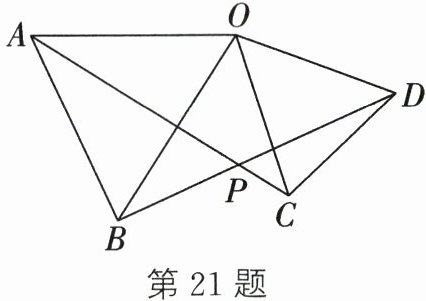
21. (8分)(2024秋·南通海门区校级期末)如图,在$\triangle AOB和\triangle COD$中,$OA= OB$,$OC= OD$,$\angle AOB= \angle COD= 50^{\circ}$.
(1) 求证:$AC= BD$;
(2) $AC与BD相交于点P$,求$\angle APB$的度数.

答案： （1）证明：$\because \angle AOB = \angle COD$，
$\therefore \angle AOB + \angle BOC = \angle COD + \angle BOC$，即$\angle AOC = \angle BOD$。
$\because OA = OB$，$OC = OD$，
$\therefore \triangle AOC \cong \triangle BOD(SAS)$。
$\therefore AC = BD$。
（2）解：设$AC$与$BO$交于点$M$，则$\angle AMO = \angle BMP$。
$\because \triangle AOC \cong \triangle BOD$，
$\therefore \angle OAC = \angle OBD$。
$\because 180^{\circ} - \angle OAC - \angle AMO = 180^{\circ} - \angle OBD - \angle BMP$，
$\therefore \angle MPB = \angle AOM = 50^{\circ}$。
$\therefore \angle APB = 50^{\circ}$。