《2025年轻松作业本八年级数学上册人教版》

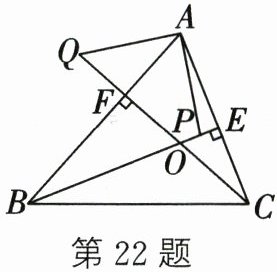
22. (8分)如图,$BE$、$CF是\triangle ABC$的高,在射线$BE上截取BP= AC$,在射线$CF上截取CQ= AB$.求证:
(1) $AP= QA$;
(2) $AP\perp AQ$.

答案： 证明：（1）
∵CF⊥AB，BE⊥AC，
∴∠AEB=∠AFC=90°，
∴∠ABP=90°-∠BAC，∠QCA=90°-∠BAC，
∴∠ABP=∠QCA，
在△APB和△QAC中，
$\left\{\begin{array}{l} BP=CA\\ \angle ABP=\angle QCA\\ BA=CQ\end{array}\right.$，
∴△APB≌△QAC（SAS），
∴AP=QA；
（2）
∵△APB≌△QAC，
∴∠BAP=∠CQA，
∵CF⊥AB，
∴∠CQA+∠QAF=90°，
∴∠BAP+∠QAF=90°，
即∠QAP=90°，
∴AP⊥AQ．

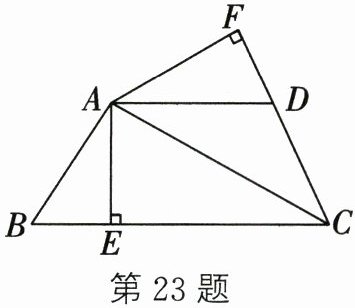
23. (10分)如图,四边形$ABCD$中,$AB= AD$,$AC平分\angle BCD$,$AE\perp BC于E$,$AF\perp CD交CD的延长线于F$.
(1) 求证:$\triangle ABE\cong \triangle ADF$;
(2) 求证:$BC-CD= 2BE$;
(3) 请直接写出$BC+CD与CE$之间的数量关系______(不证明).

（1）证明：∵AC平分∠BCD，AE⊥BC，AF⊥CD，
∴AE=AF，∠AEB=∠AFD=90°。
在Rt△ABE和Rt△ADF中，
$\left\{\begin{array}{l} AB=AD\\ AE=AF\end{array}\right. $
∴Rt△ABE≌Rt△ADF（HL）。
（2）证明：在△ACF和△ACE中，
$\left\{\begin{array}{l} ∠F=∠AEC=90°\\ ∠ACF=∠ACE\\ AC=AC\end{array}\right. $
∴△ACF≌△ACE（AAS）。
∴CF=CE。
∵△ABE≌△ADF，
∴BE=DF。
∵BC=CE+BE，CD=CF-DF=CE-BE，
∴BC-CD=（CE+BE）-（CE-BE）=2BE。
BC+CD=2CE

答案： （1）证明：
∵AC平分∠BCD，AE⊥BC，AF⊥CD，
∴AE=AF，∠AEB=∠AFD=90°。
在Rt△ABE和Rt△ADF中，
$\left\{\begin{array}{l} AB=AD\\ AE=AF\end{array}\right. $
∴Rt△ABE≌Rt△ADF（HL）。
（2）证明：在△ACF和△ACE中，
$\left\{\begin{array}{l} ∠F=∠AEC=90°\\ ∠ACF=∠ACE\\ AC=AC\end{array}\right. $
∴△ACF≌△ACE（AAS）。
∴CF=CE。
∵△ABE≌△ADF，
∴BE=DF。
∵BC=CE+BE，CD=CF-DF=CE-BE，
∴BC-CD=（CE+BE）-（CE-BE）=2BE。
（3）BC+CD=2CE

24. (14分)【学习新知】等边对等角是等腰三角形的性质定理.如图①,可以表述为:$\because AB= AC$,$\therefore \angle B= \angle C$.
【新知应用】已知:在$\triangle ABC$中,$AB= AC$,若$\angle A= 110^{\circ}$,则$\angle B= $$35^{\circ}$;若$\angle B= 70^{\circ}$,则$\angle A= $$40^{\circ}$.
【尝试探究】如图②,四边形$ABCD$中,$AB= AD$,$\angle B+\angle ADC= 180^{\circ}$,若连接$CA$,则$CA平分\angle BCD$.
某数学小组成员通过观察、实验,提出以下想法:延长$CD到点E$,使得$DE= BC$,连接$AE$,利用三角形全等的判定和等腰三角形的性质可以证明.请你参考他们的想法,写出完整的证明过程.
证明：延长$CD$到点$E$，使得$DE=BC$，连接$AE$。
$\because \angle ADC + \angle ADE = 180^{\circ}$，$\angle B + \angle ADC = 180^{\circ}$，
$\therefore \angle B = \angle ADE$。
在$\triangle ABC$和$\triangle ADE$中，
$\left\{\begin{array}{l} AB = AD,\\ \angle B = \angle ADE,\\ BC = ED,\end{array}\right.$
$\therefore \triangle ABC\cong \triangle ADE(SAS)$。
$\therefore \angle ACB = \angle AED$，$AC = AE$。
$\because AC = AE$，
$\therefore \angle ACD = \angle E$。
$\therefore \angle ACD = \angle ACB$。
$\therefore CA$平分$\angle BCD$。
【拓展应用】借助上一问的尝试,继续探究:如图③所示,在五边形$ABCDE$中,$AB= AE$,$BC+DE= CD$,$\angle B+\angle AED= 180^{\circ}$,连接$CA$,$CA平分\angle BCD$吗? 请说明理由.
解：$CA$平分$\angle BCD$。理由如下：
延长$DE$到点$F$，使得$EF=BC$，连接$AF$。
$\because \angle AED + \angle AEF = 180^{\circ}$，$\angle B + \angle AED = 180^{\circ}$，
$\therefore \angle B = \angle AEF$。
在$\triangle ABC$和$\triangle AEF$中，
$\left\{\begin{array}{l} AB = AE,\\ \angle B = \angle AEF,\\ BC = EF,\end{array}\right.$
$\therefore \triangle ABC\cong \triangle AEF(SAS)$。
$\therefore AC = AF$，$\angle ACB = \angle F$。
$\because BC + DE = CD$，$BC = EF$，
$\therefore CD = FD$。
在$\triangle ACD$和$\triangle AFD$中，
$\left\{\begin{array}{l} AC = AF,\\ AD = AD,\\ CD = FD,\end{array}\right.$
$\therefore \triangle ACD\cong \triangle AFD(SSS)$。
$\therefore \angle ACD = \angle F$。
$\therefore \angle ACD = \angle ACB$。
$\therefore AC$平分$\angle BCD$。

答案： 【新知应用】$35^{\circ}$；$40^{\circ}$
【尝试探究】证明：延长$CD$到点$E$，使得$DE=BC$，连接$AE$。
$\because \angle ADC + \angle ADE = 180^{\circ}$，$\angle B + \angle ADC = 180^{\circ}$，
$\therefore \angle B = \angle ADE$。
在$\triangle ABC$和$\triangle ADE$中，
$\left\{\begin{array}{l} AB = AD,\\ \angle B = \angle ADE,\\ BC = ED,\end{array}\right.$
$\therefore \triangle ABC\cong \triangle ADE(SAS)$。
$\therefore \angle ACB = \angle AED$，$AC = AE$。
$\because AC = AE$，
$\therefore \angle ACD = \angle E$。
$\therefore \angle ACD = \angle ACB$。
$\therefore CA$平分$\angle BCD$。
【拓展应用】解：$CA$平分$\angle BCD$。理由如下：
延长$DE$到点$F$，使得$EF=BC$，连接$AF$。
$\because \angle AED + \angle AEF = 180^{\circ}$，$\angle B + \angle AED = 180^{\circ}$，
$\therefore \angle B = \angle AEF$。
在$\triangle ABC$和$\triangle AEF$中，
$\left\{\begin{array}{l} AB = AE,\\ \angle B = \angle AEF,\\ BC = EF,\end{array}\right.$
$\therefore \triangle ABC\cong \triangle AEF(SAS)$。
$\therefore AC = AF$，$\angle ACB = \angle F$。
$\because BC + DE = CD$，$BC = EF$，
$\therefore CD = FD$。
在$\triangle ACD$和$\triangle AFD$中，
$\left\{\begin{array}{l} AC = AF,\\ AD = AD,\\ CD = FD,\end{array}\right.$
$\therefore \triangle ACD\cong \triangle AFD(SSS)$。
$\therefore \angle ACD = \angle F$。
$\therefore \angle ACD = \angle ACB$。
$\therefore AC$平分$\angle BCD$。