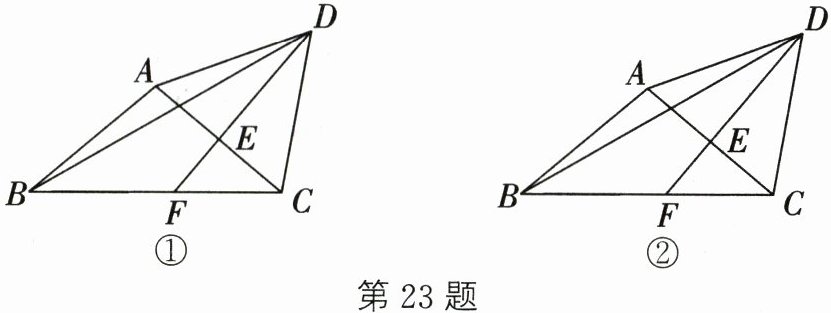
23. (10分)在△ABC中,AB= AC,在△ABC的外部作等边三角形ACD,E为AC的中点,连接DE并延长交BC于点F,连接BD.
(1) 如图①,若∠BAC= 100°,求∠BDF的度数;
(2) 如图②,∠ACB的平分线交AB于点M,交EF于点N,连接BN.
① 补全图②;
② 若BN= DN,求证:MB= MN.
(1) 如图①,若∠BAC= 100°,求∠BDF的度数;
(2) 如图②,∠ACB的平分线交AB于点M,交EF于点N,连接BN.
① 补全图②;
② 若BN= DN,求证:MB= MN.

答案:
(1)解:在等边三角形 $ACD$ 中,$\angle CAD = \angle ADC = 60^{\circ}$,$AD = AC$。$\because E$ 为 $AC$ 的中点,$\therefore \angle ADE = \frac{1}{2}\angle ADC = 30^{\circ}$。$\because AB = AC$,$\therefore AD = AB$。$\because \angle BAD = \angle BAC + \angle CAD = 160^{\circ}$,$\therefore \angle ADB = \angle ABD = 10^{\circ}$,$\therefore \angle BDF = \angle ADF - \angle ADB = 20^{\circ}$。
(2)① 补全图形如图所示; ② 证明:如图,连接 $AN$。$\because CM$ 平分 $\angle ACB$,$\therefore$ 设 $\angle ACM = \angle BCM = \alpha$。$\because AB = AC$,$\therefore \angle ABC = \angle ACB = 2\alpha$。在等边三角形 $ACD$ 中,$\because E$ 为 $AC$ 的中点,$\therefore DN \perp AC$。$\therefore NA = NC$。$\therefore \angle NAC = \angle NCA = \alpha$。$\therefore \angle DAN = 60^{\circ} + \alpha$。在 $\triangle ABN$ 和 $\triangle ADN$ 中,$\begin{cases} AB = AD \\ BN = DN \\ AN = AN \end{cases}$,$\therefore \triangle ABN \cong \triangle ADN(SSS)$。$\therefore \angle ABN = \angle ADN = 30^{\circ}$,$\angle BAN = \angle DAN = 60^{\circ} + \alpha$。$\therefore \angle BAC = 60^{\circ} + 2\alpha$。在 $\triangle ABC$ 中,$\angle BAC + \angle ACB + \angle ABC = 180^{\circ}$,$\therefore 60^{\circ} + 2\alpha + 2\alpha + 2\alpha = 180^{\circ}$,解得 $\alpha = 20^{\circ}$。$\therefore \angle NBC = \angle ABC - \angle ABN = 10^{\circ}$。$\therefore \angle MNB = \angle NBC + \angle NCB = 30^{\circ}$。$\therefore \angle MNB = \angle MBN$。$\therefore MB = MN$。

(1)解:在等边三角形 $ACD$ 中,$\angle CAD = \angle ADC = 60^{\circ}$,$AD = AC$。$\because E$ 为 $AC$ 的中点,$\therefore \angle ADE = \frac{1}{2}\angle ADC = 30^{\circ}$。$\because AB = AC$,$\therefore AD = AB$。$\because \angle BAD = \angle BAC + \angle CAD = 160^{\circ}$,$\therefore \angle ADB = \angle ABD = 10^{\circ}$,$\therefore \angle BDF = \angle ADF - \angle ADB = 20^{\circ}$。
(2)① 补全图形如图所示; ② 证明:如图,连接 $AN$。$\because CM$ 平分 $\angle ACB$,$\therefore$ 设 $\angle ACM = \angle BCM = \alpha$。$\because AB = AC$,$\therefore \angle ABC = \angle ACB = 2\alpha$。在等边三角形 $ACD$ 中,$\because E$ 为 $AC$ 的中点,$\therefore DN \perp AC$。$\therefore NA = NC$。$\therefore \angle NAC = \angle NCA = \alpha$。$\therefore \angle DAN = 60^{\circ} + \alpha$。在 $\triangle ABN$ 和 $\triangle ADN$ 中,$\begin{cases} AB = AD \\ BN = DN \\ AN = AN \end{cases}$,$\therefore \triangle ABN \cong \triangle ADN(SSS)$。$\therefore \angle ABN = \angle ADN = 30^{\circ}$,$\angle BAN = \angle DAN = 60^{\circ} + \alpha$。$\therefore \angle BAC = 60^{\circ} + 2\alpha$。在 $\triangle ABC$ 中,$\angle BAC + \angle ACB + \angle ABC = 180^{\circ}$,$\therefore 60^{\circ} + 2\alpha + 2\alpha + 2\alpha = 180^{\circ}$,解得 $\alpha = 20^{\circ}$。$\therefore \angle NBC = \angle ABC - \angle ABN = 10^{\circ}$。$\therefore \angle MNB = \angle NBC + \angle NCB = 30^{\circ}$。$\therefore \angle MNB = \angle MBN$。$\therefore MB = MN$。

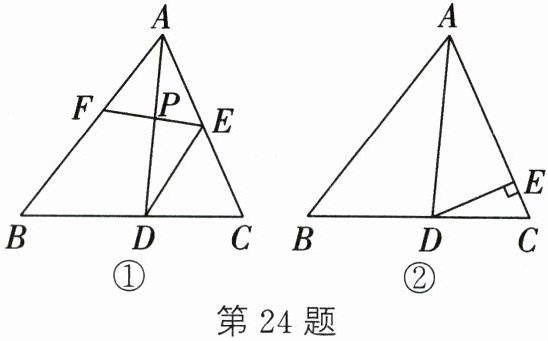
24. (12分)在△ABC中,∠BAC= 70°,AD是△ABC的角平分线,点E是AC边上的一点,点F为直线AB上的一动点,连接EF,直线EF与直线AD交于点P,设∠AEF= α°.
(1) 如图①,若DE//AB,则:
① ∠ADE的度数是______;
② 当∠DPE= ∠DEP时,∠AEF= ______度;当∠PDE= ∠PED时,∠AEF= ______度.
(2) 如图②,若DE⊥AC,则是否存在这样的α的值,使得△DPE中有两个相等的角? 若存在,求出α的值;若不存在,说明理由.
(1) 如图①,若DE//AB,则:
① ∠ADE的度数是______;
② 当∠DPE= ∠DEP时,∠AEF= ______度;当∠PDE= ∠PED时,∠AEF= ______度.
(2) 如图②,若DE⊥AC,则是否存在这样的α的值,使得△DPE中有两个相等的角? 若存在,求出α的值;若不存在,说明理由.

答案:
(1)① $35^{\circ}$ ② $37.5$ $75$ (2)在 $Rt\triangle ADE$ 中,$\angle ADE = 90^{\circ} - 35^{\circ} = 55^{\circ}$。① 当 $DP = DE$ 时,$\angle DPE = 62.5^{\circ}$,$\angle AEF = \angle DPE - \angle DAC = 62.5^{\circ} - 35^{\circ} = 27.5^{\circ}$。② 当 $EP = ED$ 时,$\angle EPD = \angle ADE = 55^{\circ}$,$\angle AEF = \angle DPE - \angle DAC = 55^{\circ} - 35^{\circ} = 20^{\circ}$。③ 当 $DP = PE$ 时,$\angle EPD = 180^{\circ} - 2×55^{\circ} = 70^{\circ}$,$\angle AEF = \angle DPE - \angle DAC = 70^{\circ} - 35^{\circ} = 35^{\circ}$。④ 如图②中,当点 $F$ 在 $BA$ 的延长线上时,只有 $DE = DP$,此时 $\angle AEF = 90^{\circ} - 27.5^{\circ} = 62.5^{\circ}$。

(1)① $35^{\circ}$ ② $37.5$ $75$ (2)在 $Rt\triangle ADE$ 中,$\angle ADE = 90^{\circ} - 35^{\circ} = 55^{\circ}$。① 当 $DP = DE$ 时,$\angle DPE = 62.5^{\circ}$,$\angle AEF = \angle DPE - \angle DAC = 62.5^{\circ} - 35^{\circ} = 27.5^{\circ}$。② 当 $EP = ED$ 时,$\angle EPD = \angle ADE = 55^{\circ}$,$\angle AEF = \angle DPE - \angle DAC = 55^{\circ} - 35^{\circ} = 20^{\circ}$。③ 当 $DP = PE$ 时,$\angle EPD = 180^{\circ} - 2×55^{\circ} = 70^{\circ}$,$\angle AEF = \angle DPE - \angle DAC = 70^{\circ} - 35^{\circ} = 35^{\circ}$。④ 如图②中,当点 $F$ 在 $BA$ 的延长线上时,只有 $DE = DP$,此时 $\angle AEF = 90^{\circ} - 27.5^{\circ} = 62.5^{\circ}$。

查看更多完整答案,请扫码查看


