《2025年轻松作业本八年级数学上册人教版》

24. (12 分)在△ABC 中,AB = AC,D 是直线 BC 上一点,以 AD 为一条边在 AD 的右侧作△ADE,使 AE = AD,∠DAE = ∠BAC,连接 CE.
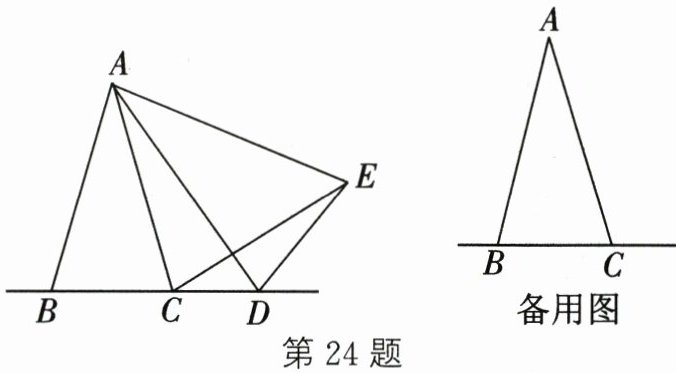
(1)如图,当点 D 在 BC 的延长线上移动时,若∠BAC = 25°,则∠DCE = ______25°；
(2)设∠BAC = α,∠DCE = β.
① 当点 D 在 BC 的延长线上移动时,α 与 β 之间有什么数量关系？请说明理由；
② 当点 D 在直线 BC 上(不与 B、C 两点重合)移动时,α 与 β 之间有什么数量关系？请直接写出你的结论.

(2)①$\alpha=\beta$，理由：$\because\angle DAE = \angle BAC$，$\therefore\angle DAE+\angle CAD=\angle BAC+\angle CAD$，即$\angle CAE=\angle BAD$。在$\triangle BAD$和$\triangle CAE$中，$\begin{cases}AB = AC\\\angle BAD=\angle CAE\\AD = AE\end{cases}$，$\therefore\triangle BAD\cong\triangle CAE(SAS)$，$\therefore\angle B=\angle ACE$。$\because\angle ACD=\angle B+\angle BAC=\angle ACE+\angle DCE$，$\therefore\angle BAC=\angle DCE$。$\because\angle BAC=\alpha$，$\angle DCE=\beta$，$\therefore\alpha=\beta$。
②当点$D$在线段$BC$上时，$\alpha+\beta=180^{\circ}$；当点$D$在$BC$的延长线或反向延长线上时，$\alpha=\beta$。

答案：
(1)$25^{\circ}$
(2)①$\alpha=\beta$，理由：$\because\angle DAE = \angle BAC$，$\therefore\angle DAE+\angle CAD=\angle BAC+\angle CAD$，即$\angle CAE=\angle BAD$。在$\triangle BAD$和$\triangle CAE$中，$\begin{cases}AB = AC\\\angle BAD=\angle CAE\\AD = AE\end{cases}$，$\therefore\triangle BAD\cong\triangle CAE(SAS)$，$\therefore\angle B=\angle ACE$。$\because\angle ACD=\angle B+\angle BAC=\angle ACE+\angle DCE$，$\therefore\angle BAC=\angle DCE$。$\because\angle BAC=\alpha$，$\angle DCE=\beta$，$\therefore\alpha=\beta$。
②当点$D$在线段$BC$上时，$\alpha+\beta=180^{\circ}$；当点$D$在$BC$的延长线或反向延长线上时，$\alpha=\beta$。

25. (12 分)从三角形一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,若分得的两个小三角形中一个三角形为等腰三角形,另一个三角形的三个内角与原来三角形的三个内角分别相等,则称这条线段叫做这个三角形的“等角分割线”. 例如,等腰直角三角形斜边上的高就是这个等腰直角三角形的一条“等角分割线”.
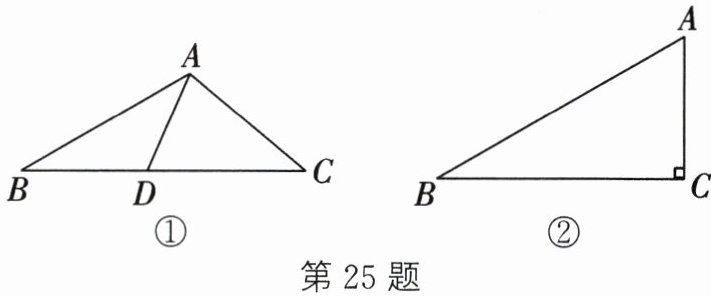
(1)如图①,在△ABC 中,D 是边 BC 上一点,若∠B = 30°,∠BAD = ∠C = 40°,求证：AD 为△ABC 的“等角分割线”；
(2)如图②,△ABC 中,∠C = 90°,∠B = 30°.
① 利用直尺和圆规,作出△ABC 的“等角分割线”,写出作法并说明理由；
② 若 BC = 3,求出①中作出的“等角分割线”的长度；
(3)在△ABC 中,∠A = 24°,若△ABC 存在“等角分割线”CD,直接写出所有符合要求的∠B 的度数.

答案：
（1）证明：$\because\angle B = 30^{\circ}$，$\angle BAD=\angle C = 40^{\circ}$，$\therefore\angle ADB=\angle BAC = 180^{\circ}-40^{\circ}-30^{\circ}=110^{\circ}$。又$\because\angle B=\angle B$，$\therefore\triangle ABD$的三个内角与$\triangle ABC$的三个内角的度数分别相等。$\because\angle B = 30^{\circ}$，$\angle BAD = 40^{\circ}$，$\therefore\angle ADC=\angle B+\angle BAD = 70^{\circ}$。又$\because\angle C = 40^{\circ}$，$\therefore\angle DAC=\angle BAC-\angle BAD = 70^{\circ}=\angle ADC$。$\therefore AC = DC$。$\therefore\triangle ACD$是等腰三角形。$\therefore AD$为$\triangle ABC$的“等角分割线”；（2）解：①画$\angle BAC$的平分线，交$BC$于点$D$，线段$AD$即为所求，如图所示。理由如下：$\because\angle C = 90^{\circ}$，$\angle B = 30^{\circ}$，$\therefore\angle BAC = 90^{\circ}-30^{\circ}=60^{\circ}$。$\because AD$平分$\angle BAC$，$\therefore\angle DAC=\angle DAB = 30^{\circ}=\angle B$。$\therefore\angle ADC = 60^{\circ}=\angle BAC$。又$\because\angle C=\angle C$，$\therefore\triangle ADC$的三个内角与$\triangle ABC$的三个内角分别相等。$\because\angle BAD=\angle B$，$\therefore AD = BD$。$\therefore\triangle ABD$是等腰三角形，$\therefore AD$为$\triangle ABC$的“等角分割线”；②设$CD = x$，$\because\triangle ADC$中，$\angle C = 90^{\circ}$，$\angle DAC = 30^{\circ}$，$\therefore AD = 2CD = 2x$。$\therefore BD = AD = 2x$。$\because BC = 3$，$\therefore x + 2x = 3$。$\therefore x = 1$。$\therefore AD = 2x = 2$；（3）解：当$\triangle ACD$是等腰三角形，$DA = DC$时，$\angle ACD=\angle A = 24^{\circ}$，$\therefore\angle ACB=\angle BDC = 24^{\circ}+24^{\circ}=48^{\circ}$。$\therefore\angle B = 180^{\circ}-24^{\circ}-48^{\circ}=108^{\circ}$；当$\triangle ACD$是等腰三角形，$DA = AC$时，$\angle ACD=\angle ADC=\frac{1}{2}(180^{\circ}-24^{\circ})=78^{\circ}$，$\angle BCD=\angle A = 24^{\circ}$，$\therefore\angle ACB = 78^{\circ}+24^{\circ}=102^{\circ}$。$\therefore\angle B = 180^{\circ}-24^{\circ}-102^{\circ}=54^{\circ}$；当$\triangle BCD$是等腰三角形，$DC = BD$时，$\angle ACD=\angle BCD=\angle B=\frac{1}{3}(180^{\circ}-24^{\circ})=52^{\circ}$；当$\triangle BCD$是等腰三角形，$DB = BC$时，$\angle BDC=\angle BCD$，设$\angle BDC=\angle BCD = x$，则$\angle B = 180^{\circ}-2x$，则$\angle ACD=\angle B = 180^{\circ}-2x$，由题意得，$180^{\circ}-2x + 24^{\circ}=x$，解得，$x = 68^{\circ}$，$\therefore\angle B = 180^{\circ}-2x = 44^{\circ}$。综上所述，$\angle B$的度数为$108^{\circ}$或$54^{\circ}$或$52^{\circ}$或$44^{\circ}$。