9. 定义:一个三角形的一边长是另一边长的 2 倍,这样的三角形叫做“倍长三角形”. 若等腰△ABC 是“倍长三角形”,底边 BC 的长为 3,则腰 AB 的长为______
6
.
答案:
解:因为等腰△ABC是“倍长三角形”,底边BC=3,所以分两种情况讨论:
情况一:若腰AB是底边BC的2倍,则AB=2×3=6。此时三边长为6,6,3,满足三角形三边关系(6+3>6,6+6>3)。
情况二:若底边BC是腰AB的2倍,则AB=3÷2=1.5。此时三边长为1.5,1.5,3,因为1.5+1.5=3,不满足三角形三边关系(两边之和大于第三边),所以舍去。
综上,腰AB的长为6。
答案:6
情况一:若腰AB是底边BC的2倍,则AB=2×3=6。此时三边长为6,6,3,满足三角形三边关系(6+3>6,6+6>3)。
情况二:若底边BC是腰AB的2倍,则AB=3÷2=1.5。此时三边长为1.5,1.5,3,因为1.5+1.5=3,不满足三角形三边关系(两边之和大于第三边),所以舍去。
综上,腰AB的长为6。
答案:6
10. 等腰三角形的一个内角为 70°,则另外两个内角的度数分别是
55°、55°或70°、40°
.
答案:
当70°为顶角时,底角为$(180^{\circ}-70^{\circ})÷2=55^{\circ}$,另外两个内角为$55^{\circ}$、$55^{\circ}$;
当70°为底角时,顶角为$180^{\circ}-70^{\circ}×2=40^{\circ}$,另外两个内角为$70^{\circ}$、$40^{\circ}$。
综上,另外两个内角的度数分别是$55^{\circ}$、$55^{\circ}$或$70^{\circ}$、$40^{\circ}$。
当70°为底角时,顶角为$180^{\circ}-70^{\circ}×2=40^{\circ}$,另外两个内角为$70^{\circ}$、$40^{\circ}$。
综上,另外两个内角的度数分别是$55^{\circ}$、$55^{\circ}$或$70^{\circ}$、$40^{\circ}$。
11. 如图,在△ABC 中,D 是边 AB 上的动点,在边 AC、BC 上分别有点 E、F,使得 AE = AD,BF = BD. 若∠C = α,则∠EDF =
$90^{\circ}-\frac{1}{2}\alpha$
.
答案:
1. 首先,在$\triangle ABC$中,根据三角形内角和定理:
因为$\angle A+\angle B+\angle C = 180^{\circ}$,所以$\angle A+\angle B=180^{\circ}-\angle C = 180^{\circ}-\alpha$。
2. 然后,在$\triangle ADE$中,$AE = AD$,根据等腰三角形的性质:
设$\angle ADE=\angle AED$,由三角形内角和定理$\angle A+\angle ADE+\angle AED = 180^{\circ}$,则$\angle ADE=\frac{1}{2}(180^{\circ}-\angle A)=90^{\circ}-\frac{1}{2}\angle A$。
3. 接着,在$\triangle BDF$中,$BF = BD$,同理:
设$\angle BDF=\angle BFD$,由三角形内角和定理$\angle B+\angle BDF+\angle BFD = 180^{\circ}$,则$\angle BDF=\frac{1}{2}(180^{\circ}-\angle B)=90^{\circ}-\frac{1}{2}\angle B$。
4. 最后,求$\angle EDF$:
因为$\angle ADE+\angle EDF+\angle BDF = 180^{\circ}$,所以$\angle EDF=180^{\circ}-\angle ADE - \angle BDF$。
把$\angle ADE = 90^{\circ}-\frac{1}{2}\angle A$,$\angle BDF = 90^{\circ}-\frac{1}{2}\angle B$代入上式得:
$\angle EDF=180^{\circ}-(90^{\circ}-\frac{1}{2}\angle A)-(90^{\circ}-\frac{1}{2}\angle B)$。
去括号得$\angle EDF = 180^{\circ}-90^{\circ}+\frac{1}{2}\angle A - 90^{\circ}+\frac{1}{2}\angle B$。
整理得$\angle EDF=\frac{1}{2}(\angle A+\angle B)$。
又因为$\angle A+\angle B = 180^{\circ}-\alpha$,所以$\angle EDF = 90^{\circ}-\frac{1}{2}\alpha$。
故答案为$90^{\circ}-\frac{1}{2}\alpha$。
因为$\angle A+\angle B+\angle C = 180^{\circ}$,所以$\angle A+\angle B=180^{\circ}-\angle C = 180^{\circ}-\alpha$。
2. 然后,在$\triangle ADE$中,$AE = AD$,根据等腰三角形的性质:
设$\angle ADE=\angle AED$,由三角形内角和定理$\angle A+\angle ADE+\angle AED = 180^{\circ}$,则$\angle ADE=\frac{1}{2}(180^{\circ}-\angle A)=90^{\circ}-\frac{1}{2}\angle A$。
3. 接着,在$\triangle BDF$中,$BF = BD$,同理:
设$\angle BDF=\angle BFD$,由三角形内角和定理$\angle B+\angle BDF+\angle BFD = 180^{\circ}$,则$\angle BDF=\frac{1}{2}(180^{\circ}-\angle B)=90^{\circ}-\frac{1}{2}\angle B$。
4. 最后,求$\angle EDF$:
因为$\angle ADE+\angle EDF+\angle BDF = 180^{\circ}$,所以$\angle EDF=180^{\circ}-\angle ADE - \angle BDF$。
把$\angle ADE = 90^{\circ}-\frac{1}{2}\angle A$,$\angle BDF = 90^{\circ}-\frac{1}{2}\angle B$代入上式得:
$\angle EDF=180^{\circ}-(90^{\circ}-\frac{1}{2}\angle A)-(90^{\circ}-\frac{1}{2}\angle B)$。
去括号得$\angle EDF = 180^{\circ}-90^{\circ}+\frac{1}{2}\angle A - 90^{\circ}+\frac{1}{2}\angle B$。
整理得$\angle EDF=\frac{1}{2}(\angle A+\angle B)$。
又因为$\angle A+\angle B = 180^{\circ}-\alpha$,所以$\angle EDF = 90^{\circ}-\frac{1}{2}\alpha$。
故答案为$90^{\circ}-\frac{1}{2}\alpha$。
12. 如图,正六边形 ABCDEF 的顶点 A、F 分别在正方形 BMGH 的边 BH、GH 上. 若正方形 BMGH 的边长为 6,则正六边形 ABCDEF 的边长为______
4
.
答案:
1. 首先,设正六边形$ABCDEF$的边长为$x$:
因为正六边形$ABCDEF$的内角和公式为$(n - 2)×180^{\circ}$($n = 6$),则内角$\angle BAF=\frac{(6 - 2)×180^{\circ}}{6}=120^{\circ}$。
那么$\angle FAH = 180^{\circ}-\angle BAF=60^{\circ}$。
在$Rt\triangle AFH$中,$\angle AFH = 30^{\circ}$($\angle FAH = 60^{\circ}$,$\angle H = 90^{\circ}$)。
根据直角三角形中$30^{\circ}$所对的直角边是斜边的一半,可得$AH=\frac{1}{2}AF=\frac{1}{2}x$。
2. 然后,根据正方形$BMGH$的边长$BH = 6$:
又因为$BH=BA + AH$,且$BA=x$,$AH=\frac{1}{2}x$。
所以$x+\frac{1}{2}x = 6$。
3. 最后,解方程:
合并同类项得$\frac{2x + x}{2}=6$,即$\frac{3x}{2}=6$。
两边同时乘以$\frac{2}{3}$,解得$x = 4$。
故正六边形$ABCDEF$的边长为$4$。
因为正六边形$ABCDEF$的内角和公式为$(n - 2)×180^{\circ}$($n = 6$),则内角$\angle BAF=\frac{(6 - 2)×180^{\circ}}{6}=120^{\circ}$。
那么$\angle FAH = 180^{\circ}-\angle BAF=60^{\circ}$。
在$Rt\triangle AFH$中,$\angle AFH = 30^{\circ}$($\angle FAH = 60^{\circ}$,$\angle H = 90^{\circ}$)。
根据直角三角形中$30^{\circ}$所对的直角边是斜边的一半,可得$AH=\frac{1}{2}AF=\frac{1}{2}x$。
2. 然后,根据正方形$BMGH$的边长$BH = 6$:
又因为$BH=BA + AH$,且$BA=x$,$AH=\frac{1}{2}x$。
所以$x+\frac{1}{2}x = 6$。
3. 最后,解方程:
合并同类项得$\frac{2x + x}{2}=6$,即$\frac{3x}{2}=6$。
两边同时乘以$\frac{2}{3}$,解得$x = 4$。
故正六边形$ABCDEF$的边长为$4$。
13. 若点 P 关于 x 轴对称的点为$ P_1(2a + 1,-a + 1),$且点$ P_1 $在一、三象限的角平分线上,则点 P 的坐标为______
$(1,-1)$
.
答案:
解:因为点$P_1(2a + 1,-a + 1)$在一、三象限的角平分线上,所以横纵坐标相等,即$2a + 1=-a + 1$。
解得$3a=0$,$a=0$。
则$2a + 1=1$,$-a + 1=1$,所以$P_1$的坐标为$(1,1)$。
因为点$P$与$P_1$关于$x$轴对称,所以点$P$的坐标为$(1,-1)$。
$(1,-1)$
解得$3a=0$,$a=0$。
则$2a + 1=1$,$-a + 1=1$,所以$P_1$的坐标为$(1,1)$。
因为点$P$与$P_1$关于$x$轴对称,所以点$P$的坐标为$(1,-1)$。
$(1,-1)$
14. 如图,在△ABC 中,AB = AC,CD = CB. 若∠ACD = 40°,则∠BAC = ______.
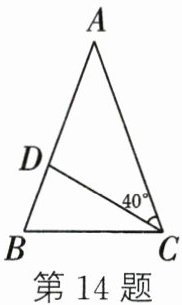

$\frac{100}{3}^{\circ}$
答案:
解:设∠BAC = x。
∵AB = AC,
∴∠ABC = ∠ACB = $\frac{180^{\circ} - x}{2} = 90^{\circ} - \frac{x}{2}$。
∵∠ACD = 40°,
∴∠BCD = ∠ACB - ∠ACD = $90^{\circ} - \frac{x}{2} - 40^{\circ} = 50^{\circ} - \frac{x}{2}$。
∵CD = CB,
∴∠CDB = ∠CBD = ∠ABC = $90^{\circ} - \frac{x}{2}$。
在△BCD中,∠BCD + ∠CBD + ∠CDB = 180°,
即$50^{\circ} - \frac{x}{2} + 2(90^{\circ} - \frac{x}{2}) = 180^{\circ}$,
解得$x = (\frac{100}{3})^{\circ}$。
$(\frac{100}{3})^{\circ}$
∵AB = AC,
∴∠ABC = ∠ACB = $\frac{180^{\circ} - x}{2} = 90^{\circ} - \frac{x}{2}$。
∵∠ACD = 40°,
∴∠BCD = ∠ACB - ∠ACD = $90^{\circ} - \frac{x}{2} - 40^{\circ} = 50^{\circ} - \frac{x}{2}$。
∵CD = CB,
∴∠CDB = ∠CBD = ∠ABC = $90^{\circ} - \frac{x}{2}$。
在△BCD中,∠BCD + ∠CBD + ∠CDB = 180°,
即$50^{\circ} - \frac{x}{2} + 2(90^{\circ} - \frac{x}{2}) = 180^{\circ}$,
解得$x = (\frac{100}{3})^{\circ}$。
$(\frac{100}{3})^{\circ}$
15. 如图,在△ABC 中,AC = 8,BC = 5,AB 的垂直平分线 DE 交 AB 于点 D,交边 AC 于点 E,则△BCE 的周长为______.


13
答案:
∵DE是AB的垂直平分线,
∴AE = BE。
∵AC = 8,
∴AE + EC = 8,即BE + EC = 8。
∵BC = 5,
∴△BCE的周长 = BE + EC + BC = 8 + 5 = 13。
13
∵DE是AB的垂直平分线,
∴AE = BE。
∵AC = 8,
∴AE + EC = 8,即BE + EC = 8。
∵BC = 5,
∴△BCE的周长 = BE + EC + BC = 8 + 5 = 13。
13
16. 若等腰三角形的两边长分别为 x cm 和(2x - 6)cm,且周长为 17 cm,则第三边的长为______
5cm 或$\frac{11}{2}cm$或$\frac{28}{5}cm$
.
答案:
1. 分情况讨论:
情况一:当$x = 2x−6$时:
解方程$x = 2x−6$,移项可得$2x−x = 6$,即$x = 6$。
则三边分别为$x = 6cm$,$2x−6 = 6cm$,第三边$y=17-(6 + 6)=5cm$。
此时$6 + 5>6$,$6+6>5$,满足三角形三边关系(任意两边之和大于第三边)。
情况二:当$x$为腰长时:
则$2x+(2x - 6)=17$,
去括号得$2x+2x−6 = 17$,
移项合并同类项:$4x=17 + 6$,即$4x=23$,解得$x=\frac{23}{4}$。
则$2x−6=2×\frac{23}{4}-6=\frac{23}{2}-6=\frac{23 - 12}{2}=\frac{11}{2}$。
三边分别为$\frac{23}{4}cm$,$\frac{23}{4}cm$,$\frac{11}{2}cm$,因为$\frac{23}{4}+\frac{11}{2}=\frac{23 + 22}{4}=\frac{45}{4}>\frac{23}{4}$,$\frac{23}{4}+\frac{23}{4}=\frac{23}{2}>\frac{11}{2}$,满足三角形三边关系。
情况三:当$2x−6$为腰长时:
则$2(2x - 6)+x = 17$。
去括号得$4x-12 + x = 17$。
移项合并同类项:$5x=17 + 12$,即$5x=29$,解得$x=\frac{29}{5}$。
则$2x−6=2×\frac{29}{5}-6=\frac{58}{5}-6=\frac{58 - 30}{5}=\frac{28}{5}$。
三边分别为$\frac{29}{5}cm$,$\frac{28}{5}cm$,$\frac{28}{5}cm$,因为$\frac{29}{5}+\frac{28}{5}=\frac{57}{5}>\frac{28}{5}$,$\frac{28}{5}+\frac{28}{5}=\frac{56}{5}>\frac{29}{5}$,满足三角形三边关系。
2. 综上:
第三边的长为$5cm$或$\frac{11}{2}cm$或$\frac{28}{5}cm$。
故答案为$5cm$或$\frac{11}{2}cm$或$\frac{28}{5}cm$。
情况一:当$x = 2x−6$时:
解方程$x = 2x−6$,移项可得$2x−x = 6$,即$x = 6$。
则三边分别为$x = 6cm$,$2x−6 = 6cm$,第三边$y=17-(6 + 6)=5cm$。
此时$6 + 5>6$,$6+6>5$,满足三角形三边关系(任意两边之和大于第三边)。
情况二:当$x$为腰长时:
则$2x+(2x - 6)=17$,
去括号得$2x+2x−6 = 17$,
移项合并同类项:$4x=17 + 6$,即$4x=23$,解得$x=\frac{23}{4}$。
则$2x−6=2×\frac{23}{4}-6=\frac{23}{2}-6=\frac{23 - 12}{2}=\frac{11}{2}$。
三边分别为$\frac{23}{4}cm$,$\frac{23}{4}cm$,$\frac{11}{2}cm$,因为$\frac{23}{4}+\frac{11}{2}=\frac{23 + 22}{4}=\frac{45}{4}>\frac{23}{4}$,$\frac{23}{4}+\frac{23}{4}=\frac{23}{2}>\frac{11}{2}$,满足三角形三边关系。
情况三:当$2x−6$为腰长时:
则$2(2x - 6)+x = 17$。
去括号得$4x-12 + x = 17$。
移项合并同类项:$5x=17 + 12$,即$5x=29$,解得$x=\frac{29}{5}$。
则$2x−6=2×\frac{29}{5}-6=\frac{58}{5}-6=\frac{58 - 30}{5}=\frac{28}{5}$。
三边分别为$\frac{29}{5}cm$,$\frac{28}{5}cm$,$\frac{28}{5}cm$,因为$\frac{29}{5}+\frac{28}{5}=\frac{57}{5}>\frac{28}{5}$,$\frac{28}{5}+\frac{28}{5}=\frac{56}{5}>\frac{29}{5}$,满足三角形三边关系。
2. 综上:
第三边的长为$5cm$或$\frac{11}{2}cm$或$\frac{28}{5}cm$。
故答案为$5cm$或$\frac{11}{2}cm$或$\frac{28}{5}cm$。
17. 如图,△ABC 是边长为 3 的等边三角形,△BDC 是等腰三角形,且∠BDC = 120°,以 D 为顶点作一个 60°角,使其两边分别交 AB、AC 于点 M、N,连接 MN,则△AMN 的周长为______.
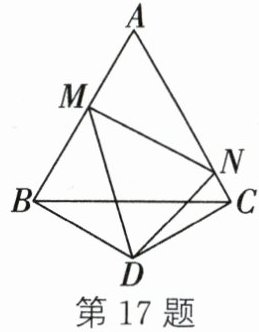

答案:
解:延长AC至E,使CE=BM,连接DE。
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°。
∵△BDC是等腰三角形,∠BDC=120°,
∴BD=CD,∠DBC=∠DCB=30°,
∴∠ABD=∠ACD=90°,
∴∠DCE=180°-∠ACD=90°=∠ABD。
在△MBD和△ECD中,
$\left\{\begin{array}{l} BM=CE\\ ∠MBD=∠ECD\\ BD=CD\end{array}\right.$
∴△MBD≌△ECD(SAS),
∴MD=ED,∠MDB=∠EDC。
∵∠BDC=120°,∠MDN=60°,
∴∠MDB+∠NDC=60°,
∴∠EDC+∠NDC=∠EDN=60°=∠MDN。
在△MDN和△EDN中,
$\left\{\begin{array}{l} MD=ED\\ ∠MDN=∠EDN\\ DN=DN\end{array}\right.$
∴△MDN≌△EDN(SAS),
∴MN=EN=CN+CE=CN+BM。
∵△AMN的周长=AM+AN+MN=AM+AN+BM+CN=(AM+BM)+(AN+CN)=AB+AC,
又
∵AB=AC=3,
∴△AMN的周长=3+3=6。
6
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°。
∵△BDC是等腰三角形,∠BDC=120°,
∴BD=CD,∠DBC=∠DCB=30°,
∴∠ABD=∠ACD=90°,
∴∠DCE=180°-∠ACD=90°=∠ABD。
在△MBD和△ECD中,
$\left\{\begin{array}{l} BM=CE\\ ∠MBD=∠ECD\\ BD=CD\end{array}\right.$
∴△MBD≌△ECD(SAS),
∴MD=ED,∠MDB=∠EDC。
∵∠BDC=120°,∠MDN=60°,
∴∠MDB+∠NDC=60°,
∴∠EDC+∠NDC=∠EDN=60°=∠MDN。
在△MDN和△EDN中,
$\left\{\begin{array}{l} MD=ED\\ ∠MDN=∠EDN\\ DN=DN\end{array}\right.$
∴△MDN≌△EDN(SAS),
∴MN=EN=CN+CE=CN+BM。
∵△AMN的周长=AM+AN+MN=AM+AN+BM+CN=(AM+BM)+(AN+CN)=AB+AC,
又
∵AB=AC=3,
∴△AMN的周长=3+3=6。
6
18. 如图,在 Rt△ABC 中,∠C = 90°,以△ABC 的一边为边画等腰三角形,使得它的第三个顶点在△ABC 的其他边上,则可以画出的不同的等腰三角形的个数最多为
7
.
答案:
解:以AC为腰:
- 以A为顶点,在AB上取点D,使AD=AC;
- 以C为顶点,在AB上取点D,使CD=AC。
以BC为腰:
- 以B为顶点,在AB上取点D,使BD=BC;
- 以C为顶点,在AB上取点D,使CD=BC。
以AB为腰:
- 以A为顶点,在BC上取点D,使AD=AB;
- 以B为顶点,在AC上取点D,使BD=AB。
以AB为底:
- 在AB上取中点D,连接CD,CD=AD=BD。
综上,共7个不同的等腰三角形。
7
- 以A为顶点,在AB上取点D,使AD=AC;
- 以C为顶点,在AB上取点D,使CD=AC。
以BC为腰:
- 以B为顶点,在AB上取点D,使BD=BC;
- 以C为顶点,在AB上取点D,使CD=BC。
以AB为腰:
- 以A为顶点,在BC上取点D,使AD=AB;
- 以B为顶点,在AC上取点D,使BD=AB。
以AB为底:
- 在AB上取中点D,连接CD,CD=AD=BD。
综上,共7个不同的等腰三角形。
7
19. (7 分)(2024·长沙中考)如图,点 C 在线段 AD 上,AB = AD,∠B = ∠D,BC = DE.
(2)若∠BAC = 60°,求∠ACE 的度数.

(2)若∠BAC = 60°,求∠ACE 的度数.

答案:
(1)证明:在$\triangle ABC$和$\triangle ADE$中,$\begin{cases}BC = DE,\\\angle B=\angle D,\\AB = AD,\end{cases}\therefore\triangle ABC\cong\triangle ADE(SAS)$;
(2)解:由(1)得$\triangle ABC\cong\triangle ADE$,$\therefore AC = AE$,$\angle BAC=\angle DAE = 60^{\circ}$,$\therefore\angle AEC=\angle ACE$,$\because\angle AEC+\angle ACE+\angle DAE=180^{\circ}$,$\therefore2\angle ACE=180^{\circ}-60^{\circ}=120^{\circ}$,$\therefore\angle ACE = 60^{\circ}$。
(2)解:由(1)得$\triangle ABC\cong\triangle ADE$,$\therefore AC = AE$,$\angle BAC=\angle DAE = 60^{\circ}$,$\therefore\angle AEC=\angle ACE$,$\because\angle AEC+\angle ACE+\angle DAE=180^{\circ}$,$\therefore2\angle ACE=180^{\circ}-60^{\circ}=120^{\circ}$,$\therefore\angle ACE = 60^{\circ}$。
20. (7 分)如图,点 C 在线段 AD 上,AB = AD,∠B = ∠D,BC = DE.
(1)求证:△ABC ≌ △ADE;
(2)若∠BAC = 60°,求∠ACE 的度数.
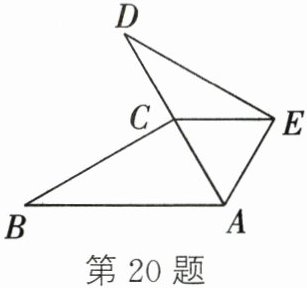
(1)求证:△ABC ≌ △ADE;
(2)若∠BAC = 60°,求∠ACE 的度数.

答案:
(1)证明:在$\triangle ABC$和$\triangle ADE$中,
$\begin{cases}BC = DE,\\\angle B = \angle D,\\AB = AD,\end{cases}$
$\therefore\triangle ABC\cong\triangle ADE(\text{SAS})$。
(2)解:由(1)得$\triangle ABC\cong\triangle ADE$,
$\therefore AC = AE$,$\angle BAC=\angle DAE = 60^{\circ}$,
$\therefore\triangle ACE$是等腰三角形,
$\therefore\angle ACE=\angle AEC$,
$\because\angle ACE+\angle AEC+\angle DAE=180^{\circ}$,
$\therefore2\angle ACE + 60^{\circ}=180^{\circ}$,
$\therefore\angle ACE = 60^{\circ}$。
$\begin{cases}BC = DE,\\\angle B = \angle D,\\AB = AD,\end{cases}$
$\therefore\triangle ABC\cong\triangle ADE(\text{SAS})$。
(2)解:由(1)得$\triangle ABC\cong\triangle ADE$,
$\therefore AC = AE$,$\angle BAC=\angle DAE = 60^{\circ}$,
$\therefore\triangle ACE$是等腰三角形,
$\therefore\angle ACE=\angle AEC$,
$\because\angle ACE+\angle AEC+\angle DAE=180^{\circ}$,
$\therefore2\angle ACE + 60^{\circ}=180^{\circ}$,
$\therefore\angle ACE = 60^{\circ}$。
查看更多完整答案,请扫码查看


