《2025年轻松作业本八年级数学上册人教版》

1. 在下列长度的四条线段中,能与长为6 cm,8 cm的两条线段围成一个三角形的是(C)
A.1 cm
B.2 cm
C.13 cm
D.14 cm

答案： 解：设第三边长度为$x$cm，根据三角形三边关系，两边之和大于第三边，两边之差小于第三边，可得：
$8 - 6 ＜ x ＜ 8 + 6$，即$2 ＜ x ＜ 14$。
选项中只有13cm满足条件，故选C。

2. 如图,$\triangle ABC$中边AB上的高为(B)
A.AD
B.CE
C.AF
D.BG

答案： 在△ABC中，边AB上的高是从顶点C向AB所在直线作的垂线段。观察图形，CE垂直于AB，所以边AB上的高为CE。
答案：B

3. 直角三角形的两个锐角的平分线所夹的锐角是(C)
A.$30^{\circ}$
B.$60^{\circ}$
C.$45^{\circ}$
D.$15^{\circ}或75^{\circ}$

答案： 解：设直角三角形为$Rt\triangle ABC$，$\angle C=90^{\circ}$，则$\angle A+\angle B=90^{\circ}$。
设$AD$、$BE$分别为$\angle A$、$\angle B$的平分线，交点为$O$。
$\angle OAB=\frac{1}{2}\angle A$，$\angle OBA=\frac{1}{2}\angle B$。
在$\triangle AOB$中，$\angle AOB=180^{\circ}-(\angle OAB+\angle OBA)=180^{\circ}-\frac{1}{2}(\angle A+\angle B)=180^{\circ}-\frac{1}{2}×90^{\circ}=135^{\circ}$。
两平分线所夹锐角为$180^{\circ}-\angle AOB=180^{\circ}-135^{\circ}=45^{\circ}$。
答案：C

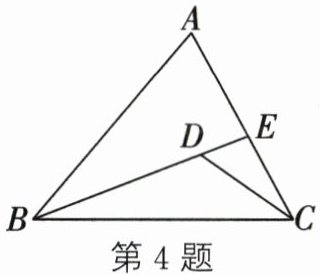
4. 如图,若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有(B)

A.2对
B.3对
C.4对
D.6对

答案： 以BC为公共边的“共边三角形”有：
1. △ABC与△DBC；
2. △ABC与△EBC；
3. △DBC与△EBC。
共有3对。
答案：B

5. 如图,巡逻艇C在军舰A的北偏东$62^{\circ}$方向上,且在军舰B的北偏东$13^{\circ}$方向上,军舰B位于军舰A的正东方向,则$\angle ACB$的度数为(C)
A.$13^{\circ}$
B.$26^{\circ}$
C.$49^{\circ}$
D.$62^{\circ}$

答案： 解：由题意得，军舰B位于军舰A的正东方向，巡逻艇C在军舰A的北偏东$62^{\circ}$方向上，所以$\angle CAN = 62^{\circ}$（N为正北方向），则$\angle CAB = 90^{\circ}-62^{\circ}=28^{\circ}$。
巡逻艇C在军舰B的北偏东$13^{\circ}$方向上，所以$\angle CBM = 13^{\circ}$（M为正北方向），则$\angle CBA = 90^{\circ}+13^{\circ}=103^{\circ}$。
在$\triangle ABC$中，$\angle ACB = 180^{\circ}-\angle CAB-\angle CBA = 180^{\circ}-28^{\circ}-103^{\circ}=49^{\circ}$。
答案：C

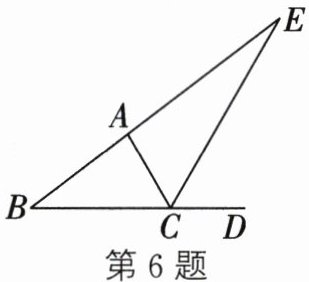
6. 如图,$\triangle ABC的外角\angle ACD$的平分线CE交BA的延长线于点E,若$\angle BCA = 60^{\circ}$,则$\angle B+\angle E$的值是(B)

A.$59^{\circ}$
B.$60^{\circ}$
C.$61^{\circ}$
D.$62^{\circ}$

答案： 解：
∵∠BCA=60°，∠ACB+∠ACD=180°，
∴∠ACD=180°-60°=120°.
∵CE平分∠ACD，
∴∠ACE=∠ECD=60°.
∵∠ECD是△BCE的外角，
∴∠ECD=∠B+∠E.
∴∠B+∠E=60°.
答案：B

7. 在$\triangle ABC$中,$\angle A= \frac{1}{2}\angle B= \frac{1}{3}\angle C$,则此三角形是(B)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形

答案： 设∠A = x，则∠B = 2x，∠C = 3x。
∵∠A + ∠B + ∠C = 180°，
∴x + 2x + 3x = 180°，
6x = 180°，
x = 30°。
∴∠A = 30°，∠B = 60°，∠C = 90°。
此三角形是直角三角形。
答案：B

8. 如图,在$\triangle ABC$中,$\angle BAC = 36^{\circ}$,$\angle ACB = 62^{\circ}$,BE平分$\angle ABC$,D为BE延长线上一点,且$DF\perp AC$于点F,则$\angle BDF$的度数为(C)
A.$8^{\circ}$
B.$12^{\circ}$
C.$13^{\circ}$
D.$15^{\circ}$

答案： 解：在$\triangle ABC$中，$\angle ABC=180^{\circ}-\angle BAC-\angle ACB=180^{\circ}-36^{\circ}-62^{\circ}=82^{\circ}$。
∵BE平分$\angle ABC$，
∴$\angle CBE=\frac{1}{2}\angle ABC=41^{\circ}$。
在$\triangle BEC$中，$\angle BEC=180^{\circ}-\angle CBE-\angle ACB=180^{\circ}-41^{\circ}-62^{\circ}=77^{\circ}$。
∵$\angle DEF=\angle BEC=77^{\circ}$，$DF\perp AC$，
∴$\angle DFE=90^{\circ}$。
在$\triangle DEF$中，$\angle BDF=180^{\circ}-\angle DEF-\angle DFE=180^{\circ}-77^{\circ}-90^{\circ}=13^{\circ}$。
答案：C

9. 如图,AD、BE、CF为$\triangle ABC$的三条角平分线,它们交于点O,则$\angle DOC与\angle ABE$的关系是(B)
A.相等
B.互余
C.互补
D.无法判断

答案： 解：因为$AD$、$BE$、$CF$为$\triangle ABC$的三条角平分线，
所以$\angle BAD = \frac{1}{2}\angle BAC$，$\angle ABE=\frac{1}{2}\angle ABC$ ，$\angle ACD=\frac{1}{2}\angle ACB$。
在$\triangle AOC$中，$\angle DOC$是$\triangle AOC$的外角，根据三角形外角性质：三角形的一个外角等于不相邻的两个内角之和，
所以$\angle DOC=\angle OAC + \angle OCA$（$\angle OAC=\frac{1}{2}\angle BAC$，$\angle OCA = \frac{1}{2}\angle ACB$）。
又因为在$\triangle ABC$中，$\angle BAC+\angle ABC+\angle ACB = 180^{\circ}$，即$\angle BAC+\angle ACB=180^{\circ}-\angle ABC$。
那么$\angle DOC=\frac{1}{2}(\angle BAC + \angle ACB)=\frac{1}{2}(180^{\circ}-\angle ABC)=90^{\circ}-\frac{1}{2}\angle ABC$。
因为$\angle ABE=\frac{1}{2}\angle ABC$，所以$\angle DOC + \angle ABE=90^{\circ}$。
所以$\angle DOC$与$\angle ABE$互余，答案是B。