《2025年轻松作业本八年级数学上册人教版》

24. (9分)材料一：一个大于1的正整数,若被$N$除余1,被$(N - 1)$除余1,被$(N - 2)$除余1,…,被3除余1,被2除余1,那么称这个正整数为“明$N$礼”数($N$取最大),例如：73(被5除余3)被4除余1,被3除余1,被2除余1,那么73为“明四礼”数.
材料二：设$N$,$(N - 1)$,$(N - 2)$,…,3,2的最小公倍数为$k$,那么“明$N$礼”数可以表示为$kn + 1$($n$为正整数),例如：6,5,4,3,2的最小公倍数为60,那么“明六礼”数可以表示为$60n + 1$($n$为正整数).
(1)17______不是“明三礼”数(填“是”或“不是”)；721是“明______六礼”数；
(2)求出最小的三位“明三礼”数；
解：3和2的最小公倍数是6，设“明三礼”数为$6n + 1$（$n$为正整数）。
要使$6n + 1$为最小三位数，则$6n + 1\geq100$，解得$n\geq16.5$。
$n$取最小正整数17，$6×17 + 1 = 103$。
(3)一个“明三礼”数与一个“明四礼”数的和为32,求出这两个数.
解：3和2的最小公倍数是6，设“明三礼”数为$6m + 1$（$m$为正整数）；
4、3、2的最小公倍数是12，设“明四礼”数为$12n + 1$（$n$为正整数）。
由题意得$6m + 1 + 12n + 1 = 32$，化简得$m + 2n = 5$。
$m$、$n$为正整数，解得$\begin{cases}m=1\\n=2\end{cases}$或$\begin{cases}m=3\\n=1\end{cases}$。
当$m=1$，$n=2$时，“明三礼”数为7，“明四礼”数为25；
当$m=3$，$n=1$时，“明三礼”数为19，“明四礼”数为13。

答案： （1）不是 六
（2）解：3和2的最小公倍数是6，设“明三礼”数为$6n + 1$（$n$为正整数）。
要使$6n + 1$为最小三位数，则$6n + 1\geq100$，解得$n\geq16.5$。
$n$取最小正整数17，$6×17 + 1 = 103$。
（3）解：3和2的最小公倍数是6，设“明三礼”数为$6m + 1$（$m$为正整数）；
4、3、2的最小公倍数是12，设“明四礼”数为$12n + 1$（$n$为正整数）。
由题意得$6m + 1 + 12n + 1 = 32$，化简得$m + 2n = 5$。
$m$、$n$为正整数，解得$\begin{cases}m=1\\n=2\end{cases}$或$\begin{cases}m=3\\n=1\end{cases}$。
当$m=1$，$n=2$时，“明三礼”数为7，“明四礼”数为25；
当$m=3$，$n=1$时，“明三礼”数为19，“明四礼”数为13。

25. (9分)(2024秋·南通崇川区校级期中)我们学过单项式除以单项式、多项式除以单项式,那么多项式除以多项式该怎么计算呢？我们也可以用竖式进行类似演算,即先把被除式、除式按某个字母降幂排列,并把所缺的项用零补齐(或留出空白),再类似于数的竖式除法求出商式和余式,其中余式为0或余式的次数低于除式的次数.
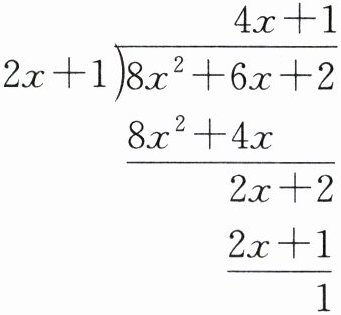
例如：计算$(8x^{2}+6x + 2)÷(2x + 1)$,可用如图的竖式进行计算.因此商式是$4x + 1$,余式是1.
(1)计算$(3x^{2}+10x + 4)÷(x + 3)$,商式是______,余式是______；
(2)计算$(a^{2}+ab - 2b^{2})÷(a - b)$,结果为______；
(3)已知$M$是一个整式,$m$是常数,$x\neq - 1$,$M(x + 1)= x^{2}+mx + 36$,求$m$的值.

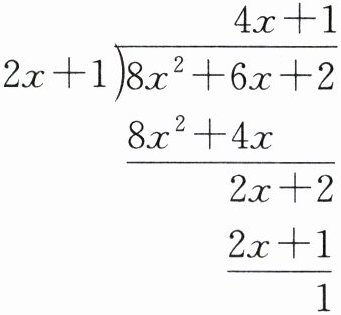
答案：
（1）$3x + 1$ 1 （2）$a + 2b$ （3）$\because M$是一个整式，$m$是常数，$x\neq -1$，$M(x + 1)=x^{2}+mx + 36$，$\therefore M=(x^{2}+mx + 36)÷(x + 1)$，列竖式计算如下：

$\because M$是一个整式，$\therefore 37 - m = 0$，$\therefore m = 37$。