24. (9分)对于任意四个有理数a、b、c、d,可以组成两个有理数对$ ( a , b ) 与 ( c , d ) $.我们规定:$ ( a , b ) \otimes ( c , d ) = a ^ { 2 } + d ^ { 2 } - b c $.例如:$ ( 1 , 2 ) \otimes ( 3 , 4 ) = 1 ^ { 2 } + 4 ^ { 2 } - 2 × 3 = 11 $.
(1)若$ ( 2 x , k x ) \otimes ( y , - y ) $是一个完全平方式,求常数k的值;
(2)若$ 2 x + y = 12 $,且$ ( 3 x + y , 2 x ^ { 2 } + 3 y ^ { 2 } ) \otimes ( 3 , x - 3 y ) = 104 $,求xy的值;
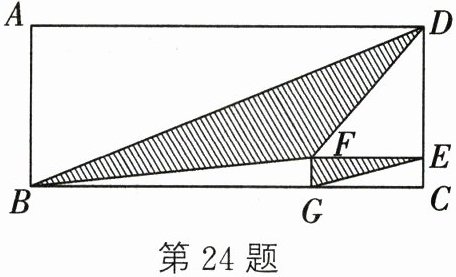
(3)在(2)的条件下,将长方形ABCD及长方形CEFG按照如图方式放置,其中点E、G分别在边CD、BC上,连接BD、BF、DF、EG.若$ A B = 2 x , B C = 8 x , C E = y , C G = 4 y $,求图中阴影部分的面积.
(1)若$ ( 2 x , k x ) \otimes ( y , - y ) $是一个完全平方式,求常数k的值;
(2)若$ 2 x + y = 12 $,且$ ( 3 x + y , 2 x ^ { 2 } + 3 y ^ { 2 } ) \otimes ( 3 , x - 3 y ) = 104 $,求xy的值;
(3)在(2)的条件下,将长方形ABCD及长方形CEFG按照如图方式放置,其中点E、G分别在边CD、BC上,连接BD、BF、DF、EG.若$ A B = 2 x , B C = 8 x , C E = y , C G = 4 y $,求图中阴影部分的面积.

答案:
(1) $(2x,kx)\otimes(y,-y)=(2x)^2+(-y)^2 - kx\cdot y=4x^2 + y^2 - kxy$,
$\because 4x^2 - kxy + y^2$是完全平方式,
$\therefore -k=\pm4$,即$k=\pm4$。
(2) $(3x+y,2x^2+3y^2)\otimes(3,x-3y)=(3x+y)^2+(x-3y)^2 - 3(2x^2+3y^2)$
$=9x^2+6xy+y^2+x^2-6xy+9y^2-6x^2-9y^2=4x^2+y^2$,
$\because 4x^2+y^2=(2x+y)^2-4xy$,且$2x+y=12$,
$\therefore 12^2 - 4xy=104$,即$144 - 4xy=104$,
解得$xy=10$。
(3) $S_{\triangle BDC}=\frac{1}{2}\cdot AB\cdot BC=\frac{1}{2}\cdot2x\cdot8x=8x^2$,
$S_{\triangle BGF}=\frac{1}{2}\cdot(B C - C G)\cdot C E=\frac{1}{2}(8x - 4y)\cdot y=4xy - 2y^2$,
$S_{\triangle DEF}=\frac{1}{2}\cdot C G\cdot(C D - C E)=\frac{1}{2}\cdot4y\cdot(2x - y)=4xy - 2y^2$,
$S_{\triangle GEC}=\frac{1}{2}\cdot C G\cdot C E=\frac{1}{2}\cdot4y\cdot y=2y^2$,
$S_{阴}=S_{\triangle BDC}-S_{\triangle BGF}-S_{\triangle DEF}-S_{\triangle GEC}$
$=8x^2-(4xy - 2y^2)-(4xy - 2y^2)-2y^2=8x^2 - 8xy + 2y^2$
$=2(4x^2 - 4xy + y^2)=2[(2x + y)^2 - 8xy]$,
$\because 2x + y=12$,$xy=10$,
$\therefore S_{阴}=2(12^2 - 8×10)=2(144 - 80)=128$。
(1) $(2x,kx)\otimes(y,-y)=(2x)^2+(-y)^2 - kx\cdot y=4x^2 + y^2 - kxy$,
$\because 4x^2 - kxy + y^2$是完全平方式,
$\therefore -k=\pm4$,即$k=\pm4$。
(2) $(3x+y,2x^2+3y^2)\otimes(3,x-3y)=(3x+y)^2+(x-3y)^2 - 3(2x^2+3y^2)$
$=9x^2+6xy+y^2+x^2-6xy+9y^2-6x^2-9y^2=4x^2+y^2$,
$\because 4x^2+y^2=(2x+y)^2-4xy$,且$2x+y=12$,
$\therefore 12^2 - 4xy=104$,即$144 - 4xy=104$,
解得$xy=10$。
(3) $S_{\triangle BDC}=\frac{1}{2}\cdot AB\cdot BC=\frac{1}{2}\cdot2x\cdot8x=8x^2$,
$S_{\triangle BGF}=\frac{1}{2}\cdot(B C - C G)\cdot C E=\frac{1}{2}(8x - 4y)\cdot y=4xy - 2y^2$,
$S_{\triangle DEF}=\frac{1}{2}\cdot C G\cdot(C D - C E)=\frac{1}{2}\cdot4y\cdot(2x - y)=4xy - 2y^2$,
$S_{\triangle GEC}=\frac{1}{2}\cdot C G\cdot C E=\frac{1}{2}\cdot4y\cdot y=2y^2$,
$S_{阴}=S_{\triangle BDC}-S_{\triangle BGF}-S_{\triangle DEF}-S_{\triangle GEC}$
$=8x^2-(4xy - 2y^2)-(4xy - 2y^2)-2y^2=8x^2 - 8xy + 2y^2$
$=2(4x^2 - 4xy + y^2)=2[(2x + y)^2 - 8xy]$,
$\because 2x + y=12$,$xy=10$,
$\therefore S_{阴}=2(12^2 - 8×10)=2(144 - 80)=128$。
25. (9分)阅读理解:
若一个整数能表示成$ a ^ { 2 } + b ^ { 2 } $(a、b为整数)的形式,则称这个数为“平和数”,例如:因为$ 5 = 2 ^ { 2 } + 1 ^ { 2 } $,所以5是“平和数”.
(1)请你直接写出2个“平和数”,判断104是否为“平和数”,并说明理由;
(2)无论x,y取何整数,代数式$ x ^ { 2 } + 9 y ^ { 2 } + 6 x - 6 y + k $(k是常数)的值都是“平和数”,求k的值;
(3)如果数m,n都是“平和数”,试说明mn也是“平和数”.
若一个整数能表示成$ a ^ { 2 } + b ^ { 2 } $(a、b为整数)的形式,则称这个数为“平和数”,例如:因为$ 5 = 2 ^ { 2 } + 1 ^ { 2 } $,所以5是“平和数”.
(1)请你直接写出2个“平和数”,判断104是否为“平和数”,并说明理由;
(2)无论x,y取何整数,代数式$ x ^ { 2 } + 9 y ^ { 2 } + 6 x - 6 y + k $(k是常数)的值都是“平和数”,求k的值;
(3)如果数m,n都是“平和数”,试说明mn也是“平和数”.
答案:
(1)2是平和数,因为$2=1^{2}+1^{2}$;34是平和数,因为$34=5^{2}+3^{2}$。104是平和数,因为$104=10^{2}+2^{2}$。
(2)$x^{2}+9y^{2}+6x - 6y + k=(x + 3)^{2}+(3y - 1)^{2}+k - 10$,因为代数式的值都是平和数,所以$k - 10=0$,解得$k=10$。
(3)设$m=a^{2}+b^{2}$,$n=c^{2}+d^{2}$($a,b,c,d$为整数),则$mn=(a^{2}+b^{2})(c^{2}+d^{2})=(ac + bd)^{2}+(ad - bc)^{2}$。因为$a,b,c,d$为整数,所以$ac + bd$,$ad - bc$是整数,所以$mn$是平和数。
(2)$x^{2}+9y^{2}+6x - 6y + k=(x + 3)^{2}+(3y - 1)^{2}+k - 10$,因为代数式的值都是平和数,所以$k - 10=0$,解得$k=10$。
(3)设$m=a^{2}+b^{2}$,$n=c^{2}+d^{2}$($a,b,c,d$为整数),则$mn=(a^{2}+b^{2})(c^{2}+d^{2})=(ac + bd)^{2}+(ad - bc)^{2}$。因为$a,b,c,d$为整数,所以$ac + bd$,$ad - bc$是整数,所以$mn$是平和数。
查看更多完整答案,请扫码查看


