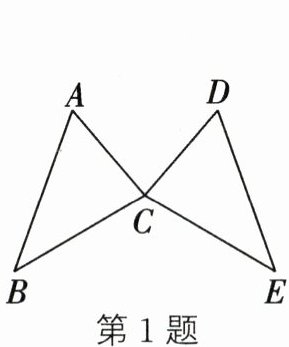
1. (2024·济南中考)如图,已知$\triangle ABC\cong \triangle DEC$,$\angle A= 60^{\circ}$,$\angle B= 40^{\circ}$,则$\angle DCE$的度数为(
A.$40^{\circ}$
B.$60^{\circ}$
C.$80^{\circ}$
D.$100^{\circ}$
C
)
A.$40^{\circ}$
B.$60^{\circ}$
C.$80^{\circ}$
D.$100^{\circ}$
答案:
在△ABC中,∠A=60°,∠B=40°,
∠ACB=180°-∠A-∠B=180°-60°-40°=80°.
∵△ABC≌△DEC,
∴∠DCE=∠ACB=80°.
答案:C
∠ACB=180°-∠A-∠B=180°-60°-40°=80°.
∵△ABC≌△DEC,
∴∠DCE=∠ACB=80°.
答案:C
2. 如图,小敏做了一个角平分仪$ABCD$,其中$AB= AD$,$BC= DC$,将仪器上的点$A与\angle PRQ的顶点R$重合,调整$AB和AD$,使它们分别落在角的两边上,过点$A$、$C画一条射线AE$,$AE就是\angle PRQ$的平分线.此角平分仪的画图原理是:根据仪器结构,可得$\triangle ABC\cong \triangle ADC$,这样就有$\angle QAE= \angle PAE$,则说明这两个三角形全等的依据是(
A.$SAS$
B.$ASA$
C.$AAS$
D.$SSS$
D
)A.$SAS$
B.$ASA$
C.$AAS$
D.$SSS$
答案:
在△ABC和△ADC中,
AB=AD,
BC=DC,
AC=AC(公共边),
所以△ABC≌△ADC(SSS)。
D
AB=AD,
BC=DC,
AC=AC(公共边),
所以△ABC≌△ADC(SSS)。
D
3. 如图,在$\triangle ABC$中,$AB= AC$,$\angle ABC$、$\angle ACB的平分线BD$、$CE相交于点O$,且$BD交AC于点D$,$CE交AB于点E$.某同学分析图形后得出以下结论:①$\triangle BCD\cong \triangle CBE$;②$\triangle BAD\cong \triangle BCD$;③$\triangle BDA\cong \triangle CEA$;④$\triangle BOE\cong \triangle COD$;⑤$\triangle ACE\cong \triangle BCE$.上述结论一定正确的是(
A.①②③
B.②③④
C.①③⑤
D.①③④
D
)A.①②③
B.②③④
C.①③⑤
D.①③④
答案:
解:
∵AB=AC,
∴∠ABC=∠ACB。
BD、CE分别平分∠ABC、∠ACB,
∴∠ABD=∠CBD=∠ACE=∠BCE。
①在△BCD和△CBE中,
∠BCD=∠CBE,BC=CB,∠CBD=∠BCE,
∴△BCD≌△CBE(ASA),①正确。
②△BAD与△BCD中,AB=AC≠BC,∠BAD≠∠BCD,②错误。
③在△BDA和△CEA中,
AB=AC,∠BAD=∠CAE,∠ABD=∠ACE,
∴△BDA≌△CEA(ASA),③正确。
④由①得BE=CD,在△BOE和△COD中,
∠OBE=∠OCD,∠BOE=∠COD,BE=CD,
∴△BOE≌△COD(AAS),④正确。
⑤∠ACE=∠BCE,但AC≠BC,⑤错误。
综上,①③④正确。
答案:D
∵AB=AC,
∴∠ABC=∠ACB。
BD、CE分别平分∠ABC、∠ACB,
∴∠ABD=∠CBD=∠ACE=∠BCE。
①在△BCD和△CBE中,
∠BCD=∠CBE,BC=CB,∠CBD=∠BCE,
∴△BCD≌△CBE(ASA),①正确。
②△BAD与△BCD中,AB=AC≠BC,∠BAD≠∠BCD,②错误。
③在△BDA和△CEA中,
AB=AC,∠BAD=∠CAE,∠ABD=∠ACE,
∴△BDA≌△CEA(ASA),③正确。
④由①得BE=CD,在△BOE和△COD中,
∠OBE=∠OCD,∠BOE=∠COD,BE=CD,
∴△BOE≌△COD(AAS),④正确。
⑤∠ACE=∠BCE,但AC≠BC,⑤错误。
综上,①③④正确。
答案:D
4. 如图,在$\triangle ABC$中,$\angle C= 90^{\circ}$,$AD是\angle BAC$的平分线,$E是边AB$上一点.若$CD= 6$,则$DE$的长可以是(
A.1
B.3
C.5
D.7
D
)A.1
B.3
C.5
D.7
答案:
解:过点D作DF⊥AB于点F。
∵AD是∠BAC的平分线,∠C=90°,
∴DF=CD=6。
∵DE是点D到直线AB上一点E的距离,
∴DE≥DF(垂线段最短),即DE≥6。
选项中只有7≥6,
故选D。
∵AD是∠BAC的平分线,∠C=90°,
∴DF=CD=6。
∵DE是点D到直线AB上一点E的距离,
∴DE≥DF(垂线段最短),即DE≥6。
选项中只有7≥6,
故选D。
5. 如图,$OA= OB$,$OC= OD$,$\angle O= 50^{\circ}$,$\angle D= 35^{\circ}$,则$\angle AEC$的度数为(
A.$60^{\circ}$
B.$50^{\circ}$
C.$45^{\circ}$
D.$30^{\circ}$
A
)A.$60^{\circ}$
B.$50^{\circ}$
C.$45^{\circ}$
D.$30^{\circ}$
答案:
解:在△OAD和△OBC中,
∵OA=OB,∠O=∠O,OD=OC,
∴△OAD≌△OBC(SAS),
∴∠C=∠D=35°。
在△OAD中,∠OAD=180°-∠O-∠D=180°-50°-35°=95°。
在△AEC中,∠AEC=180°-∠C-∠CAE=180°-35°-(180°-95°)=60°。
答案:A
∵OA=OB,∠O=∠O,OD=OC,
∴△OAD≌△OBC(SAS),
∴∠C=∠D=35°。
在△OAD中,∠OAD=180°-∠O-∠D=180°-50°-35°=95°。
在△AEC中,∠AEC=180°-∠C-∠CAE=180°-35°-(180°-95°)=60°。
答案:A
6. 如图,$AB// CD$,以点$A$为圆心,小于$AC$的长为半径画弧,分别交$AB$、$AC于E$、$F$两点;再分别以点$E$、$F$为圆心,大于$\frac{1}{2}EF$的长为半径画弧,两弧交于点$P$,作射线$AP$,交$CD于点M$.若$\angle CMA= 25^{\circ}$,则$\angle C$的度数为(
A.$100^{\circ}$
B.$110^{\circ}$
C.$120^{\circ}$
D.$130^{\circ}$
D
)A.$100^{\circ}$
B.$110^{\circ}$
C.$120^{\circ}$
D.$130^{\circ}$
答案:
解:由作图可知,AP是∠CAB的平分线。
∵AB//CD,
∴∠BAM=∠CMA=25°(两直线平行,内错角相等)。
∵AP平分∠CAB,
∴∠CAB=2∠BAM=50°。
∵AB//CD,
∴∠C+∠CAB=180°(两直线平行,同旁内角互补)。
∴∠C=180°-∠CAB=180°-50°=130°。
D
∵AB//CD,
∴∠BAM=∠CMA=25°(两直线平行,内错角相等)。
∵AP平分∠CAB,
∴∠CAB=2∠BAM=50°。
∵AB//CD,
∴∠C+∠CAB=180°(两直线平行,同旁内角互补)。
∴∠C=180°-∠CAB=180°-50°=130°。
D
查看更多完整答案,请扫码查看


