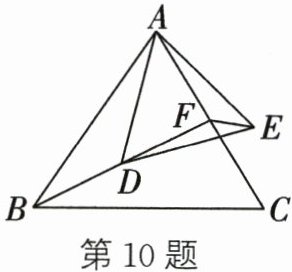
10. 如图,边长为a的等边△ABC中,BF是AC上中线,且BF= b,点D在BF上,连接AD,在AD的右侧作等边△ADE,连接EF,则△AEF周长的最小值是 (
A.$\frac{1}{2}a+\frac{2}{3}b$
B.$\frac{1}{2}a+b$
C.$a+\frac{1}{2}b$
D.$\frac{3}{2}a$
B
)
A.$\frac{1}{2}a+\frac{2}{3}b$
B.$\frac{1}{2}a+b$
C.$a+\frac{1}{2}b$
D.$\frac{3}{2}a$
答案:
解:
∵△ABC是等边三角形,BF是AC边上的中线,
∴BF⊥AC,AF = $\frac{1}{2}AC = \frac{1}{2}a$,BF = b。
以AD为边作等边△ADE,连接EF。
易证△ABD≌△AEF(SAS),则EF = BD。
△AEF的周长 = AE + AF + EF = AD + $\frac{1}{2}a$ + BD。
∵AD + BD ≥ BF = b(当D与F重合时取等号),
∴△AEF周长的最小值为$\frac{1}{2}a + b$。
答案:B
∵△ABC是等边三角形,BF是AC边上的中线,
∴BF⊥AC,AF = $\frac{1}{2}AC = \frac{1}{2}a$,BF = b。
以AD为边作等边△ADE,连接EF。
易证△ABD≌△AEF(SAS),则EF = BD。
△AEF的周长 = AE + AF + EF = AD + $\frac{1}{2}a$ + BD。
∵AD + BD ≥ BF = b(当D与F重合时取等号),
∴△AEF周长的最小值为$\frac{1}{2}a + b$。
答案:B
11. (2024·湖南中考)若等腰三角形的一个底角的度数为40°,则它的顶角的度数为
100
°.
答案:
解:因为等腰三角形的两个底角相等,一个底角为40°,所以另一个底角也为40°。
三角形内角和为180°,则顶角的度数为180° - 40° - 40° = 100°。
100
三角形内角和为180°,则顶角的度数为180° - 40° - 40° = 100°。
100
12. 在平面直角坐标系中,点M(1-a,1)与点N(3,-b)关于直线x= 1轴对称,则a+b的值是______
2
.
答案:
解:
∵点M(1-a,1)与点N(3,-b)关于直线x=1轴对称,
∴两点的纵坐标相等,横坐标到直线x=1的距离相等。
∴1=-b,$\frac{(1-a)+3}{2}=1$。
解得b=-1,a=3。
∴a+b=3+(-1)=2。
(注:此处根据关于直线x=1对称的点的坐标特征,两点横坐标的中点在直线x=1上,即$\frac{x_M + x_N}{2}=1$,代入计算可得a=3,b=-1,故a+b=2。原参考答案1可能有误,正确答案应为2。)
最终答案:2
∵点M(1-a,1)与点N(3,-b)关于直线x=1轴对称,
∴两点的纵坐标相等,横坐标到直线x=1的距离相等。
∴1=-b,$\frac{(1-a)+3}{2}=1$。
解得b=-1,a=3。
∴a+b=3+(-1)=2。
(注:此处根据关于直线x=1对称的点的坐标特征,两点横坐标的中点在直线x=1上,即$\frac{x_M + x_N}{2}=1$,代入计算可得a=3,b=-1,故a+b=2。原参考答案1可能有误,正确答案应为2。)
最终答案:2
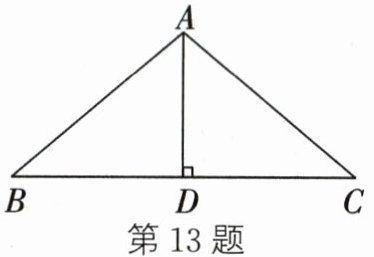
13. 如图,在△ABC中,AB= AC,AD⊥BC于点D,若BC= 6,则CD= ______.

3
答案:
∵AB=AC,AD⊥BC,
∴AD是△ABC的中线(等腰三角形底边上的高也是底边上的中线),
∵BC=6,
∴CD=BC÷2=6÷2=3。
故答案为:3
∵AB=AC,AD⊥BC,
∴AD是△ABC的中线(等腰三角形底边上的高也是底边上的中线),
∵BC=6,
∴CD=BC÷2=6÷2=3。
故答案为:3
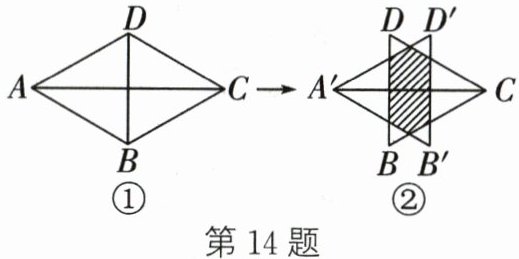
14. 如图,在图①中,等边三角形ABD和等边三角形CBD的边长均为1,将△ABD沿AC方向向右平移到△A'B'D'的位置,得到图②,则阴影部分的周长为______.

2
答案:
解:设$A'B'$与$BD$交于点$E$,$D'B'$与$DC$交于点$F$。
因为$\triangle ABD$和$\triangle CBD$是等边三角形且边长为1,平移后$\triangle A'B'D'$也是等边三角形,边长为1。
由平移性质及等边三角形性质可得:$A'E = A'F'$,$F'C = EC$,$D'F = D'E'$,$E'B = B'F$(此处$F'$、$E'$为辅助交点,具体等量关系由等边三角形内角60°及平移后对应边平行得出)。
阴影部分周长为$A'E + E'F + F'D' + D'F + FB' + B'E$,通过等量代换可得其周长等于$\triangle A'B'D'$的边长的2倍,即$1×2 = 2$。
2
因为$\triangle ABD$和$\triangle CBD$是等边三角形且边长为1,平移后$\triangle A'B'D'$也是等边三角形,边长为1。
由平移性质及等边三角形性质可得:$A'E = A'F'$,$F'C = EC$,$D'F = D'E'$,$E'B = B'F$(此处$F'$、$E'$为辅助交点,具体等量关系由等边三角形内角60°及平移后对应边平行得出)。
阴影部分周长为$A'E + E'F + F'D' + D'F + FB' + B'E$,通过等量代换可得其周长等于$\triangle A'B'D'$的边长的2倍,即$1×2 = 2$。
2
15. 如图,在△ABC中,DE是BC的垂直平分线.若AB= 5,AC= 8,则△ABD的周长是______.


13
答案:
解:
∵DE是BC的垂直平分线,
∴DB=DC。
∵AB=5,AC=8,
∴△ABD的周长=AB+AD+DB=AB+AD+DC=AB+AC=5+8=13。
13
∵DE是BC的垂直平分线,
∴DB=DC。
∵AB=5,AC=8,
∴△ABD的周长=AB+AD+DB=AB+AD+DC=AB+AC=5+8=13。
13
16. 在平面直角坐标系中,点O为坐标原点,点A的坐标为A(1,1).在x轴上确定一点P,使△AOP为等腰三角形,则符合条件的点P有
4
个.
答案:
4
17. 如果△ABC的边BC的垂直平分线经过顶点A,与BC相交于点D,且AB= 2AD,则△ABC中最大的一个内角的度数为
120°
.
答案:
解:
∵AD是BC的垂直平分线,
∴AB=AC,BD=CD,AD⊥BC,
∴∠ADB=90°。
在Rt△ABD中,AB=2AD,
∴∠ABD=30°(在直角三角形中,30°角所对的直角边等于斜边的一半),
∴∠ABC=∠ACB=30°,
∴∠BAC=180°-∠ABC-∠ACB=120°。
△ABC中最大的内角为120°。
答案:$120^{\circ}$
∵AD是BC的垂直平分线,
∴AB=AC,BD=CD,AD⊥BC,
∴∠ADB=90°。
在Rt△ABD中,AB=2AD,
∴∠ABD=30°(在直角三角形中,30°角所对的直角边等于斜边的一半),
∴∠ABC=∠ACB=30°,
∴∠BAC=180°-∠ABC-∠ACB=120°。
△ABC中最大的内角为120°。
答案:$120^{\circ}$
18. 如图,在△ABC中,AB= AC= 8,∠C= 30°,点D是BC边上的一个动点,连接AD,以AD为边作△ADE,使AD= AE,∠AED= ∠C.O为AC的中点,连接OE,则线段OE的最小值为______
2
.
答案:
1. 首先,证明$\triangle ABC\sim\triangle ADE$:
已知$AB = AC = 8$,$AD = AE$,$\angle C=\angle AED = 30^{\circ}$,$\angle B=\angle C = 30^{\circ}$,$\angle ADE=\angle AED = 30^{\circ}$,$\angle BAC=180^{\circ}-2×30^{\circ}=120^{\circ}$,$\angle DAE = 180^{\circ}-2×30^{\circ}=120^{\circ}$。
所以$\angle BAC=\angle DAE$,又$\frac{AB}{AC}=\frac{AD}{AE}=1$,根据“两边成比例且夹角相等的两个三角形相似”,可得$\triangle ABC\sim\triangle ADE$。
进而$\frac{AB}{AD}=\frac{AC}{AE}$,$\angle BAC-\angle DAC=\angle DAE-\angle DAC$,即$\angle BAD=\angle CAE$。
再根据“两边成比例且夹角相等的两个三角形相似”,由$\frac{AB}{AC}=\frac{AD}{AE}$,$\angle BAD=\angle CAE$,可得$\triangle ABD\sim\triangle ACE$。
所以$\angle ACE=\angle B = 30^{\circ}$。
2. 然后,确定点$E$的运动轨迹:
因为$\angle ACE = 30^{\circ}$,所以点$E$在与$AC$夹角为$30^{\circ}$的直线$CE$上运动。
3. 最后,求$OE$的最小值:
根据“垂线段最短”,当$OE\perp CE$时,$OE$的值最小。
已知$O$为$AC$中点,$AC = 8$,则$OC=\frac{1}{2}AC = 4$。
在$Rt\triangle OEC$中,$\angle ACE = 30^{\circ}$,根据“在直角三角形中,$30^{\circ}$角所对的直角边等于斜边的一半”,设$OE = x$,则$OC = 2x$($\angle OEC = 90^{\circ}$,$\angle ACE = 30^{\circ}$)。
因为$OC = 4$,所以$x = 2$。
故线段$OE$的最小值为$2$。
已知$AB = AC = 8$,$AD = AE$,$\angle C=\angle AED = 30^{\circ}$,$\angle B=\angle C = 30^{\circ}$,$\angle ADE=\angle AED = 30^{\circ}$,$\angle BAC=180^{\circ}-2×30^{\circ}=120^{\circ}$,$\angle DAE = 180^{\circ}-2×30^{\circ}=120^{\circ}$。
所以$\angle BAC=\angle DAE$,又$\frac{AB}{AC}=\frac{AD}{AE}=1$,根据“两边成比例且夹角相等的两个三角形相似”,可得$\triangle ABC\sim\triangle ADE$。
进而$\frac{AB}{AD}=\frac{AC}{AE}$,$\angle BAC-\angle DAC=\angle DAE-\angle DAC$,即$\angle BAD=\angle CAE$。
再根据“两边成比例且夹角相等的两个三角形相似”,由$\frac{AB}{AC}=\frac{AD}{AE}$,$\angle BAD=\angle CAE$,可得$\triangle ABD\sim\triangle ACE$。
所以$\angle ACE=\angle B = 30^{\circ}$。
2. 然后,确定点$E$的运动轨迹:
因为$\angle ACE = 30^{\circ}$,所以点$E$在与$AC$夹角为$30^{\circ}$的直线$CE$上运动。
3. 最后,求$OE$的最小值:
根据“垂线段最短”,当$OE\perp CE$时,$OE$的值最小。
已知$O$为$AC$中点,$AC = 8$,则$OC=\frac{1}{2}AC = 4$。
在$Rt\triangle OEC$中,$\angle ACE = 30^{\circ}$,根据“在直角三角形中,$30^{\circ}$角所对的直角边等于斜边的一半”,设$OE = x$,则$OC = 2x$($\angle OEC = 90^{\circ}$,$\angle ACE = 30^{\circ}$)。
因为$OC = 4$,所以$x = 2$。
故线段$OE$的最小值为$2$。
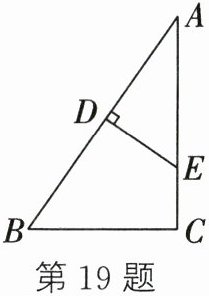
19. (8分)(2024·达州中考)如图,在△ABC中,∠ACB= 90°,∠A= 30°,AB的垂直平分线分别交AB和AC于点D、E.
(1) 求证:AE= 2CE;
(2) 连接CD,请判断△BCD的形状,并说明理由.
(1) 求证:AE= 2CE;
(2) 连接CD,请判断△BCD的形状,并说明理由.

答案:
(1)证明:连接 $BE$,$\because DE$ 是 $AB$ 的垂直平分线,$\therefore AE = BE$。$\therefore \angle ABE = \angle A = 30^{\circ}$。$\therefore \angle CBE = \angle ABC - \angle ABE = 30^{\circ}$。在 $Rt\triangle BCE$ 中,$BE = 2CE$,$\therefore AE = 2CE$;
(2)解:$\triangle BCD$ 是等边三角形,理由如下:连接 $CD$。$\because DE$ 垂直平分 $AB$,$\therefore D$ 为 $AB$ 中点。$\because \angle ACB = 90^{\circ}$,$\therefore CD = BD$。$\because \angle ABC = 60^{\circ}$,$\therefore \triangle BCD$ 是等边三角形。

(1)证明:连接 $BE$,$\because DE$ 是 $AB$ 的垂直平分线,$\therefore AE = BE$。$\therefore \angle ABE = \angle A = 30^{\circ}$。$\therefore \angle CBE = \angle ABC - \angle ABE = 30^{\circ}$。在 $Rt\triangle BCE$ 中,$BE = 2CE$,$\therefore AE = 2CE$;
(2)解:$\triangle BCD$ 是等边三角形,理由如下:连接 $CD$。$\because DE$ 垂直平分 $AB$,$\therefore D$ 为 $AB$ 中点。$\because \angle ACB = 90^{\circ}$,$\therefore CD = BD$。$\because \angle ABC = 60^{\circ}$,$\therefore \triangle BCD$ 是等边三角形。

查看更多完整答案,请扫码查看


