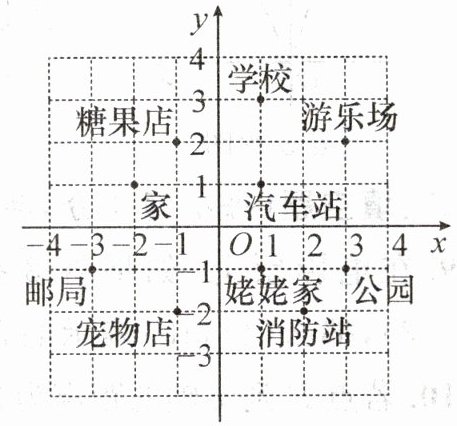
16. (8分)如图,图中标明了小英家附近的一些地方.
(1)写出汽车站和消防站的坐标.
(2)某天早晨,小英同学从家里出发,沿$(3,2),(3,-1),(1,-1),(-1,-2),(-3,-1)$的路线转了一下,又回到了家里,写出她的路线.
(1)写出汽车站和消防站的坐标.
(2)某天早晨,小英同学从家里出发,沿$(3,2),(3,-1),(1,-1),(-1,-2),(-3,-1)$的路线转了一下,又回到了家里,写出她的路线.

答案:
解:
(1)汽车站的坐标是$(1,1)$,消防站的坐标是$(2,-2)$.
(2)家→游乐场→公园→姥姥家→宠物店→邮局→家.
(1)汽车站的坐标是$(1,1)$,消防站的坐标是$(2,-2)$.
(2)家→游乐场→公园→姥姥家→宠物店→邮局→家.
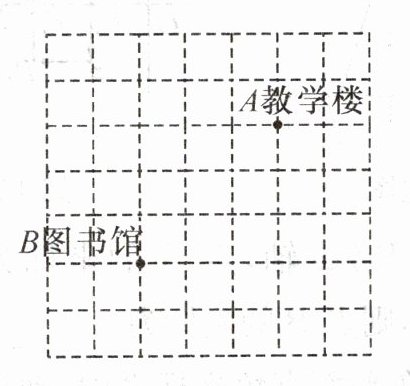
17. (10分)下图为某中学新校区分布图的一部分,方格纸中每个小方格都是边长为1个单位长度的正方形.若教学楼的坐标为$A(1,2)$,图书馆的坐标为$B(-2,-1)$,解答以下问题:
(1)在图中找到平面直角坐标系中的原点,并画出平面直角坐标系.
(2)若体育馆的坐标为$C(1,-3)$,食堂的坐标为$D(2,0)$,请在图中标出体育馆和食堂的位置.
(3)顺次连接教学楼、图书馆、体育馆、食堂,得到四边形 ABCD,求四边形 ABCD 的面积.
(1)在图中找到平面直角坐标系中的原点,并画出平面直角坐标系.
(2)若体育馆的坐标为$C(1,-3)$,食堂的坐标为$D(2,0)$,请在图中标出体育馆和食堂的位置.
(3)顺次连接教学楼、图书馆、体育馆、食堂,得到四边形 ABCD,求四边形 ABCD 的面积.

答案:
解:
(1)图略.
(2)图略.
(3)$S_{四边形ABCD}=S_{△ABC}+S_{△ACD}=\frac {1}{2}×3×5+\frac {1}{2}×1×5=10$.
(1)图略.
(2)图略.
(3)$S_{四边形ABCD}=S_{△ABC}+S_{△ACD}=\frac {1}{2}×3×5+\frac {1}{2}×1×5=10$.
18. (10分)如图所示,在平面直角坐标系中,$\triangle ABC的各顶点坐标分别为A(-1,4),B(-3,3),C(-2,1)$,直线m上每个点的横坐标都为1.
(1)画出$\triangle ABC$关于x轴对称的$\triangle A_{1}B_{1}C_{1}$.
(2)画出$\triangle ABC$关于直线m对称的$\triangle A_{2}B_{2}C_{2}$.
(3)直接写出点$M(a,b)$关于直线m对称
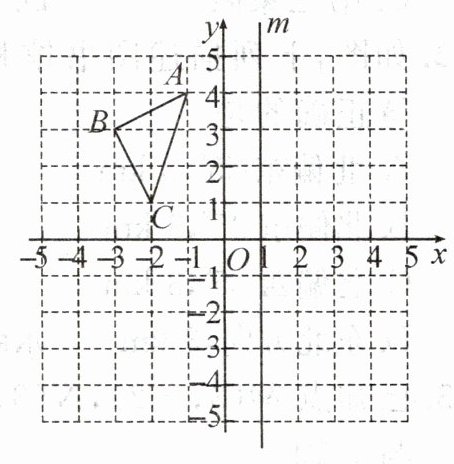
的点$M_{1}$的坐标.
(1)画出$\triangle ABC$关于x轴对称的$\triangle A_{1}B_{1}C_{1}$.
(2)画出$\triangle ABC$关于直线m对称的$\triangle A_{2}B_{2}C_{2}$.
(3)直接写出点$M(a,b)$关于直线m对称

的点$M_{1}$的坐标.
答案:
解:
(1)图略,$△A_{1}B_{1}C_{1}$即为所求.
(2)图略,$△A_{2}B_{2}C_{2}$即为所求.
(3)点$M_{1}$的坐标为$(2-a,b)$.
(1)图略,$△A_{1}B_{1}C_{1}$即为所求.
(2)图略,$△A_{2}B_{2}C_{2}$即为所求.
(3)点$M_{1}$的坐标为$(2-a,b)$.
19. (12分)如图,在平面直角坐标系xOy中,已知点$A(0,3),B(\sqrt {3},0),∠OAB= 30^{\circ }$.若对于平面内一点C,当$\triangle ABC$是以AB为腰的等腰三角形时,则称点C是线段AB的“等长点”.
(1)在点$C_{1}(0,3+2\sqrt {3}),C_{2}(-\sqrt {3},0),C_{3}(0,-\sqrt {3})$中,线段AB的“等长点”是点____.
(2)若点$D(m,n)$是线段AB的“等长点”,且$AB= AD,∠DAB= 60^{\circ }$,求m和n
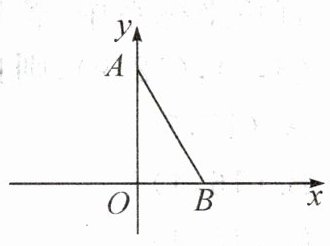
的值.
(1)在点$C_{1}(0,3+2\sqrt {3}),C_{2}(-\sqrt {3},0),C_{3}(0,-\sqrt {3})$中,线段AB的“等长点”是点____.
(2)若点$D(m,n)$是线段AB的“等长点”,且$AB= AD,∠DAB= 60^{\circ }$,求m和n

的值.
答案:
解:
(1)点$C_{1},C_{2}$
(2)在$Rt△AOB$中,$OA=3,OB=\sqrt {3},∠OAB=30^{\circ },\therefore AB=\sqrt {OA^{2}+OB^{2}}=2\sqrt {3}$.①当点 D 在 y 轴左侧时.$\because ∠DAB=60^{\circ },\therefore ∠DAO=∠DAB-∠BAO=30^{\circ }.\because AD=AB,\therefore D(-\sqrt {3},0).\therefore m=-\sqrt {3},n=0$;②当点$D'$在 y 轴右侧时.$\because ∠D'AB=60^{\circ },\therefore ∠D'AO=∠BAO+∠D'AB=90^{\circ }.\therefore n=3.\because AD'=AB=2\sqrt {3},\therefore m=2\sqrt {3}$.综上所述,$m=-\sqrt {3},n=0$或$m=2\sqrt {3},n=3$.
(1)点$C_{1},C_{2}$
(2)在$Rt△AOB$中,$OA=3,OB=\sqrt {3},∠OAB=30^{\circ },\therefore AB=\sqrt {OA^{2}+OB^{2}}=2\sqrt {3}$.①当点 D 在 y 轴左侧时.$\because ∠DAB=60^{\circ },\therefore ∠DAO=∠DAB-∠BAO=30^{\circ }.\because AD=AB,\therefore D(-\sqrt {3},0).\therefore m=-\sqrt {3},n=0$;②当点$D'$在 y 轴右侧时.$\because ∠D'AB=60^{\circ },\therefore ∠D'AO=∠BAO+∠D'AB=90^{\circ }.\therefore n=3.\because AD'=AB=2\sqrt {3},\therefore m=2\sqrt {3}$.综上所述,$m=-\sqrt {3},n=0$或$m=2\sqrt {3},n=3$.
查看更多完整答案,请扫码查看


