19. (9分)如图,正比例函数$y= kx的图象经过点A$,点$A$在第二象限,过点$A作AH⊥x$轴,垂足为$H$。已知点$A的横坐标为-3$,且$△AOH的面积为4.5$。
(1)求该正比例函数的表达式。
(2)将正比例函数$y= kx$的图象向下平移,使其恰好经过点$H$,求平移后的函数表达式。

(1)求该正比例函数的表达式。
(2)将正比例函数$y= kx$的图象向下平移,使其恰好经过点$H$,求平移后的函数表达式。

答案:
解:(1)$ \because $ 点 $ A $ 的横坐标为 $ -3 $,且 $ \triangle AOH $ 的面积为 $ 4.5 $,$ \therefore OH = 3 $,$ \frac{1}{2}OH \cdot AH = 4.5 $。$ \therefore AH = 3 $。$ \therefore $ 点 $ A $ 的坐标为 $ (-3, 3) $。$ \because $ 正比例函数 $ y = kx $ 的图象经过点 $ A $,$ \therefore -3k = 3 $,解得 $ k = -1 $。$ \therefore $ 正比例函数的表达式是 $ y = -x $。(2)$ \because AH = 3 $,$ \therefore $ 将正比例函数 $ y = -x $ 的图象向下平移 $ 3 $ 个单位长度后经过点 $ H $。$ \therefore $ 平移后的函数表达式为 $ y = -x - 3 $。
20. (10分)如图,在正方形网格中,每个小正方形的边长均为1,格点三角形$ABC$(顶点是网格线的交点的三角形)的顶点$A$,$C的坐标分别为A(-4,5)$,$C(-1,3)$。
(1)请在网格内建立符合题意的平面直角坐标系。
(2)请作出$△ABC关于y轴对称的△A_{1}B_{1}C_{1}$。
(3)写出点$B_{1}$的坐标,并求出$△A_{1}B_{1}C_{1}$的面积。

(1)请在网格内建立符合题意的平面直角坐标系。
(2)请作出$△ABC关于y轴对称的△A_{1}B_{1}C_{1}$。
(3)写出点$B_{1}$的坐标,并求出$△A_{1}B_{1}C_{1}$的面积。

答案:
解:(1)图略。(2)图略。(3)$ B_{1}(2, 1) $。$ S_{\triangle A_{1}B_{1}C_{1}} = 3 \times 4 - \frac{1}{2} \times 4 \times 2 - \frac{1}{2} \times 1 \times 2 - \frac{1}{2} \times 3 \times 2 = 12 - 4 - 1 - 3 = 4 $。
21. (10分)学完勾股定理后,小宇对勾股定理产生了极大的兴趣,通过搜集资料,他整理了一篇有关勾股定理的数学学习笔记。下面是学习笔记的部分内容,请阅读并完成相应的任务。
对勾股定理的再认识
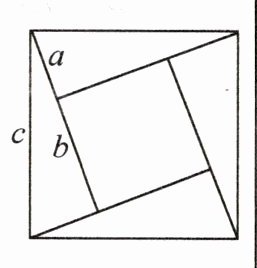
勾股定理是几何学中一颗光彩夺目的明珠,被称为“几何学的基石”。我国最早对勾股定理进行证明的是三国时期吴国的数学家赵爽。如图,这是著名的赵爽弦图,由四个全等的直角三角形拼成,用它可以验证勾股定理,思路如下:大正方形的面积有两种求法,一种是等于$c^{2}$,另一种是等于四个直角三角形与中间小正方形的面积之和,即$4×\frac {1}{2}ab+(b-a)^{2}$,从而得到等式$c^{2}= 4×\frac {1}{2}ab+(b-a)^{2}$,化简便得结论$a^{2}+b^{2}= c^{2}$。这里用两种求法来表示同一个量,从而得到等式或方程的方法,我们称之为“双求法”……
任务:请参照小论文中的“双求法”解决下列问题:
(1)图1、图2的两个正方形网格的面积分别为$S_{1}$,$S_{2}$(两个网格单位长度不同),正方形$ABCD$、正方形$MNPQ满足S_{正方形ABCD}= S_{正方形MNPQ}$。下列结论正确的是______。
A. $S_{1}= 36$
B. $S_{正方形ABCD}= \frac {4}{9}S_{1}$
C. $S_{正方形MNPQ}= \frac {5}{9}S_{2}$
D. $\frac {S_{1}}{S_{2}}= \frac {9}{10}$
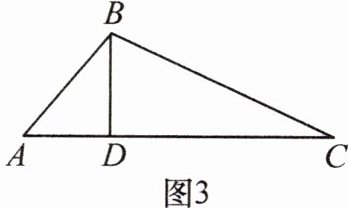
(2)如图3,在$△ABC$中,$BD是边AC$上的高,$AB= 4$,$BC= 8$,$AC= 10$,求$AD$的长。

对勾股定理的再认识
勾股定理是几何学中一颗光彩夺目的明珠,被称为“几何学的基石”。我国最早对勾股定理进行证明的是三国时期吴国的数学家赵爽。如图,这是著名的赵爽弦图,由四个全等的直角三角形拼成,用它可以验证勾股定理,思路如下:大正方形的面积有两种求法,一种是等于$c^{2}$,另一种是等于四个直角三角形与中间小正方形的面积之和,即$4×\frac {1}{2}ab+(b-a)^{2}$,从而得到等式$c^{2}= 4×\frac {1}{2}ab+(b-a)^{2}$,化简便得结论$a^{2}+b^{2}= c^{2}$。这里用两种求法来表示同一个量,从而得到等式或方程的方法,我们称之为“双求法”……
任务:请参照小论文中的“双求法”解决下列问题:
(1)图1、图2的两个正方形网格的面积分别为$S_{1}$,$S_{2}$(两个网格单位长度不同),正方形$ABCD$、正方形$MNPQ满足S_{正方形ABCD}= S_{正方形MNPQ}$。下列结论正确的是______。
A. $S_{1}= 36$
B. $S_{正方形ABCD}= \frac {4}{9}S_{1}$
C. $S_{正方形MNPQ}= \frac {5}{9}S_{2}$
D. $\frac {S_{1}}{S_{2}}= \frac {9}{10}$
(2)如图3,在$△ABC$中,$BD是边AC$上的高,$AB= 4$,$BC= 8$,$AC= 10$,求$AD$的长。



答案:
解:(1)D (2)设 $ AD = x $,则 $ CD = 10 - x $。$ \because BD $ 是边 $ AC $ 上的高,$ \therefore BD \perp AC $。$ \therefore \triangle ABD $ 和 $ \triangle BCD $ 为直角三角形。$ \therefore BD^{2} = AB^{2} - AD^{2} $,$ BD^{2} = BC^{2} - CD^{2} $。$ \therefore AB^{2} - AD^{2} = BC^{2} - CD^{2} $。$ \because AB = 4 $,$ BC = 8 $,$ \therefore 4^{2} - x^{2} = 8^{2} - (10 - x)^{2} $,解得 $ x = 2.6 $。$ \therefore AD = 2.6 $。
查看更多完整答案,请扫码查看


