《2025年名校课堂八年级数学上册北师大版》

22. (10分)如图1,这是某款新能源汽车用充电器给汽车充电时,其屏幕的起始画面。经测试,在用快速充电器和普通充电器对该汽车充电时,其电量$E(\%)与充电时间t(h)$的函数图象分别为图2中的线段$AB$,$AC$。根据以上信息,回答下列问题：
(1)在目前电量为$20\%$的情况下,用充电器给该汽车充满电时,快速充电器比普通充电器少用______$h$。
(2)求线段$AB$,$AC$的函数表达式。
(3)已知该汽车在高速公路上正常行驶时,一般情况下耗电量为每小时$20\%$。若该汽车目前电量为$20\%$,在用快速充电器将其充满电后,正常行驶$a h$,接着用普通充电器将其充满电,其“充电—耗电—充电”的时间恰好是$14h$,求$a$的值。

答案： 解：（1）8 （2）设线段 $ AB $ 的函数表达式为 $ E = k_{1}t + b_{1} $（$ k_{1} $，$ b_{1} $ 为常数，且 $ k_{1} \neq 0 $）。根据题意，得 $ b_{1} = 20 $，① $ k_{1} + b_{1} = 100 $。② 将①代入②，得 $ k_{1} + 20 = 100 $，解得 $ k_{1} = 80 $。$ \therefore $ 线段 $ AB $ 的函数表达式为 $ E = 80t + 20(0 \leq t \leq 1) $。设线段 $ AC $ 的函数表达式为 $ E = k_{2}t + b_{2} $（$ k_{2} $，$ b_{2} $ 为常数，且 $ k_{2} \neq 0 $）。根据题意，得 $ b_{2} = 20 $，① $ 9k_{2} + b_{2} = 100 $。② 将①代入②，得 $ 9k_{2} + 20 = 100 $，解得 $ k_{2} = \frac{80}{9} $。$ \therefore $ 线段 $ AC $ 的函数表达式为 $ E = \frac{80}{9}t + 20(0 \leq t \leq 9) $。（3）根据图象，用快速充电器将其充满电用时 $ 1 $ h。正常行驶 $ a $ h 后耗电 $ 20a\% $，$ \therefore $ 用普通充电器再次充满电用时 $ 20a \div \frac{80}{9} = \frac{9a}{4} $（h）。根据题意，得 $ 1 + a + \frac{9a}{4} = 14 $，解得 $ a = 4 $。

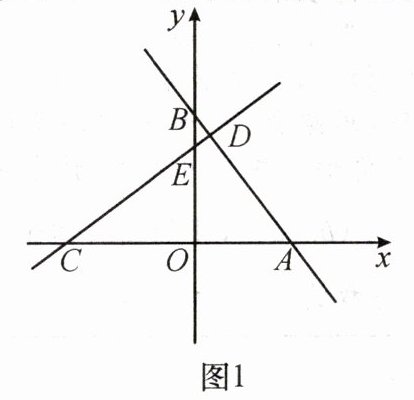
23. (11分)如图1,在平面直角坐标系中,直线$y= -\frac {4}{3}x+4分别交x$轴、$y轴于A$,$B$两点,过点$C(-4,0)作CD⊥AB于点D$,交$y轴于点E$。
(1)试说明：$△COE≌△BOA$。
(2)如图2,$M是线段CE$上一动点(不与点$C$,$E$重合),$ON⊥OM交AB于点N$,连接$MN$。
①判断$△OMN$的形状,并说明理由。


②当$△OCM与△OAN$面积相等时,求点$N$的坐标。

答案： 解：（1）把 $ x = 0 $ 代入 $ y = -\frac{4}{3}x + 4 $，得 $ y = 4 $，$ \therefore OB = 4 $。把 $ y = 0 $ 代入 $ y = -\frac{4}{3}x + 4 $，得 $ x = 3 $，$ \therefore OA = 3 $。$ \because C(-4, 0) $，$ \therefore OC = 4 $。$ \therefore OB = OC $。$ \because CD \perp AB $，$ \therefore \angle ACD + \angle CAD = 90^{\circ} $。$ \because \angle ACD + \angle OEC = 90^{\circ} $，$ \therefore \angle CAD = \angle OEC $。在 $ \triangle COE $ 和 $ \triangle BOA $ 中，$ \left\{ \begin{array}{l} \angle COE = \angle BOA \\ \angle OEC = \angle OAB \\ OC = OB \end{array} \right. $，$ \therefore \triangle COE \cong \triangle BOA $（AAS）。（2）① $ \triangle MON $ 是等腰直角三角形。理由如下：$ \because ON \perp OM $，$ \therefore \angle MON = \angle COB = 90^{\circ} $。$ \therefore \angle COM = \angle BON $。$ \because \triangle COE \cong \triangle BOA $，$ \therefore \angle OCM = \angle OBN $。在 $ \triangle COM $ 和 $ \triangle BON $ 中，$ \left\{ \begin{array}{l} \angle OCM = \angle OBN \\ OC = OB \\ \angle COM = \angle BON \end{array} \right. $，$ \therefore \triangle COM \cong \triangle BON $（ASA）。$ \therefore OM = ON $。$ \therefore \triangle MON $ 是等腰直角三角形。② $ \because \triangle COM \cong \triangle BON $，$ \triangle OCM $ 与 $ \triangle OAN $ 面积相等，$ \therefore \triangle BON $ 与 $ \triangle OAN $ 面积相等，即 $ \triangle OAN $ 面积是 $ \triangle AOB $ 面积的一半。$ \therefore \frac{1}{2} \times 3 \times y_{N} = \frac{1}{2} \times \frac{1}{2} \times 3 \times 4 $，解得 $ y_{N} = 2 $。把 $ y = 2 $ 代入 $ y = -\frac{4}{3}x + 4 $，得 $ 2 = -\frac{4}{3}x + 4 $，解得 $ x = \frac{3}{2} $。$ \therefore $ 点 $ N $ 的坐标为 $ (\frac{3}{2}, 2) $。