1. 下列各数中,是无理数的是 ()
A. $\frac{\pi}{2}$
B. $\frac{1}{3}$
C. $\sqrt[3]{27}$
D. 0.131 33
A. $\frac{\pi}{2}$
B. $\frac{1}{3}$
C. $\sqrt[3]{27}$
D. 0.131 33
答案:
A
2. 下列实数中,最小的是 ()
A. $-\sqrt{3}$
B. 1
C. 0
D. -2
A. $-\sqrt{3}$
B. 1
C. 0
D. -2
答案:
D
3. 下列各式正确的是 ()
A. $\sqrt{36}= \pm 6$
B. $-\sqrt[3]{-8}= -2$
C. $\sqrt{(-6)^2}= -6$
D. $\sqrt[3]{-7}= -\sqrt[3]{7}$
A. $\sqrt{36}= \pm 6$
B. $-\sqrt[3]{-8}= -2$
C. $\sqrt{(-6)^2}= -6$
D. $\sqrt[3]{-7}= -\sqrt[3]{7}$
答案:
D
4. 若$\sqrt{a}$是最简二次根式,则$a$可以是 ()
A. -2
B. 10
C. 12
D. 18
A. -2
B. 10
C. 12
D. 18
答案:
B
5. 下列各数中,在6和7之间的是 ()
A. $\sqrt{43}$
B. $\sqrt{28}$
C. $\sqrt[3]{39}$
D. $\sqrt{58}$
A. $\sqrt{43}$
B. $\sqrt{28}$
C. $\sqrt[3]{39}$
D. $\sqrt{58}$
答案:
A
6. 已知$a是\sqrt{81}$的平方根,$b= \sqrt{16}$,$c$是-8的立方根,则$a+b-c$的值为 ()
A. 15
B. 15或-3
C. 9
D. 9或3
A. 15
B. 15或-3
C. 9
D. 9或3
答案:
D
7. 设$\sqrt{2}= a$,$\sqrt{3}= b$,用含$a$,$b的式子表示\sqrt{0.54}$,则下列式子正确的是 ()
A. 0.3ab
B. 3ab
C. $0.1ab^2$
D. $0.1a^2b$
A. 0.3ab
B. 3ab
C. $0.1ab^2$
D. $0.1a^2b$
答案:
A
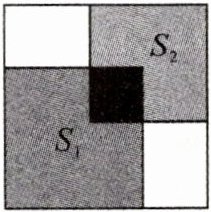
8. 如图,在大正方形纸片中放置两个小正方形(面积分别为$S_1$,$S_2$).已知$S_1= 48$,$S_2= 32$,重叠部分的面积为8,则空白部分的面积为 ()
A. $16\sqrt{6}-16$
B. $8\sqrt{6}-6$
C. $16\sqrt{6}-6$
D. $6\sqrt{6}-8$

A. $16\sqrt{6}-16$
B. $8\sqrt{6}-6$
C. $16\sqrt{6}-6$
D. $6\sqrt{6}-8$
答案:
A
9. 若一个无理数$a与\sqrt{12}$的积是一个有理数,请写出$a$的一个值:______.
答案:
$\sqrt{3}$(答案不唯一)
10. 比较大小:$\frac{\sqrt{5}-1}{2}$______$\frac{5}{8}$.(填“>”“<”或“=”)
答案:
<
11. 如图,网格中每个小正方形的边长均为1,点A,B,C,E均在小正方形的顶点上.以点A为圆心,AB的长为半径画弧,圆弧交CE于点D,则ED的长为______.


答案:
$\sqrt{5}$
12. 若$\sqrt{a-3}+(b-1)^2= 0$,则$a+b$的平方根为______.
答案:
$\pm 2$
13. 已知$m$为正整数,若$\sqrt{189m}$是整数,则根据$\sqrt{189m}= \sqrt{3×3×3×7m}= 3\sqrt{3×7m}$可知,$m有最小值3×7= 21$.设$n$为正整数,若$\sqrt{\frac{300}{n}}$是大于1的整数,则$n$的最大值为______.
答案:
75
14. (8分)计算:
(1)$\sqrt{5}×(-\sqrt{10})+(\frac{1}{7})^0+|1-\sqrt{2}|$.
(2)$(\sqrt{12}-\sqrt{3})÷2\sqrt{\frac{1}{3}}+\sqrt{27}$.
(1)$\sqrt{5}×(-\sqrt{10})+(\frac{1}{7})^0+|1-\sqrt{2}|$.
(2)$(\sqrt{12}-\sqrt{3})÷2\sqrt{\frac{1}{3}}+\sqrt{27}$.
答案:
解:
(1) 原式 $=-5 \sqrt{2}+1+\sqrt{2}-1=-4 \sqrt{2}$.
(2) 原式 $=(2 \sqrt{3}$ $-\sqrt{3}) \times \frac{\sqrt{3}}{2}+3 \sqrt{3}=\sqrt{3} \times \frac{\sqrt{3}}{2}+3 \sqrt{3}=\frac{3}{2}+3 \sqrt{3}$.
(1) 原式 $=-5 \sqrt{2}+1+\sqrt{2}-1=-4 \sqrt{2}$.
(2) 原式 $=(2 \sqrt{3}$ $-\sqrt{3}) \times \frac{\sqrt{3}}{2}+3 \sqrt{3}=\sqrt{3} \times \frac{\sqrt{3}}{2}+3 \sqrt{3}=\frac{3}{2}+3 \sqrt{3}$.
18. (12分)细心观察图形,认真分析各式,然后解答问题.
$OA_2^2= 1+(\sqrt{1})^2= 2$,$S_1= \frac{\sqrt{1}}{2}$;
$OA_3^2= 1^2+(\sqrt{2})^2= 3$,$S_2= \frac{\sqrt{2}}{2}$;
$OA_4^2= 1^2+(\sqrt{3})^2= 4$,$S_3= \frac{\sqrt{3}}{2}$;
……
(1)请用含$n$($n$是正整数)的式子表示:$OA_n^2= $______;$S_n= $______.
(2)$OA_{10}= $______.
(3)若图中某个三角形的面积是$\sqrt{5}$,计算说明它是第几个三角形.

(4)求$S_1^2+S_2^2+S_3^2+…+S_{10}^2$的值.
$OA_2^2= 1+(\sqrt{1})^2= 2$,$S_1= \frac{\sqrt{1}}{2}$;
$OA_3^2= 1^2+(\sqrt{2})^2= 3$,$S_2= \frac{\sqrt{2}}{2}$;
$OA_4^2= 1^2+(\sqrt{3})^2= 4$,$S_3= \frac{\sqrt{3}}{2}$;
……
(1)请用含$n$($n$是正整数)的式子表示:$OA_n^2= $______;$S_n= $______.
(2)$OA_{10}= $______.
(3)若图中某个三角形的面积是$\sqrt{5}$,计算说明它是第几个三角形.

(4)求$S_1^2+S_2^2+S_3^2+…+S_{10}^2$的值.
答案:
解:
(1) $n \frac{\sqrt{n}}{2}$
(2) $\sqrt{10}$
(3) 设它是第 $m$ 个三角形. 由题意,得 $\frac{\sqrt{m}}{2}=\sqrt{5}$, 解得 $m=20$. 答: 它是第 20 个三角形.
(4) $\because S_{1}^{2}=$ $\frac{1}{4}, S_{2}^{2}=\frac{2}{4}, S_{3}^{2}=\frac{3}{4}, \cdots, S_{n}^{2}=\frac{n}{4}, \therefore S_{1}^{2}+S_{2}^{2}+S_{3}^{2}+\cdots+S_{n}^{2}=$ $\frac{1}{4}+\frac{2}{4}+\cdots+\frac{n}{4}=\frac{1}{4}(1+2+\cdots+n)=\frac{1}{4} \times \frac{(1+n) n}{2}=$ $\frac{n(n+1)}{8}$. 当 $n=10$ 时, $S_{1}^{2}+S_{2}^{2}+S_{3}^{2}+\cdots+S_{10}^{2}=\frac{10 \times(10+1)}{8}=$ $\frac{55}{4}$.
(1) $n \frac{\sqrt{n}}{2}$
(2) $\sqrt{10}$
(3) 设它是第 $m$ 个三角形. 由题意,得 $\frac{\sqrt{m}}{2}=\sqrt{5}$, 解得 $m=20$. 答: 它是第 20 个三角形.
(4) $\because S_{1}^{2}=$ $\frac{1}{4}, S_{2}^{2}=\frac{2}{4}, S_{3}^{2}=\frac{3}{4}, \cdots, S_{n}^{2}=\frac{n}{4}, \therefore S_{1}^{2}+S_{2}^{2}+S_{3}^{2}+\cdots+S_{n}^{2}=$ $\frac{1}{4}+\frac{2}{4}+\cdots+\frac{n}{4}=\frac{1}{4}(1+2+\cdots+n)=\frac{1}{4} \times \frac{(1+n) n}{2}=$ $\frac{n(n+1)}{8}$. 当 $n=10$ 时, $S_{1}^{2}+S_{2}^{2}+S_{3}^{2}+\cdots+S_{10}^{2}=\frac{10 \times(10+1)}{8}=$ $\frac{55}{4}$.
查看更多完整答案,请扫码查看


