13. (8分)设三角形的三边长分别等于下列各组数,试判断各三角形是不是直角三角形.若是,指出哪一条边所对的角是直角.
(1)12,16,20.
(2)0.8,1.5,1.7.
(1)12,16,20.
(2)0.8,1.5,1.7.
答案:
解:
(1) $\because 12^{2}+16^{2}=20^{2}, \therefore$ 三角形是直角三角形, 20 这条边所对的角是直角.
(2) $\because 0.8^{2}+1.5^{2}=1.7^{2}, \therefore$ 三角形是直角三角形, 1.7 这条边所对的角是直角.
(1) $\because 12^{2}+16^{2}=20^{2}, \therefore$ 三角形是直角三角形, 20 这条边所对的角是直角.
(2) $\because 0.8^{2}+1.5^{2}=1.7^{2}, \therefore$ 三角形是直角三角形, 1.7 这条边所对的角是直角.
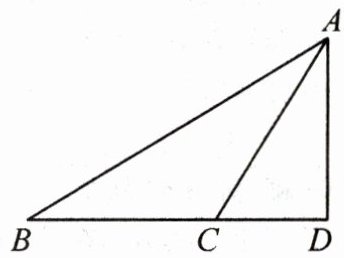
14. (8分)如图,在$△ABD$中,$∠D= 90^{\circ }$,C是BD上一点,已知$BC= 9,CD= 6,AB= 17$,求AC的长.

答案:
解: $\because B C=9, C D=6, \therefore B D=15$. 在 $\mathrm{Rt} \triangle A B D$ 中, $A D^{2}=A B^{2}-B D^{2}=64$, 在 $\mathrm{Rt} \triangle A C D$ 中, $A C^{2}=A D^{2}+C D^{2}=100, \therefore A C=10$.
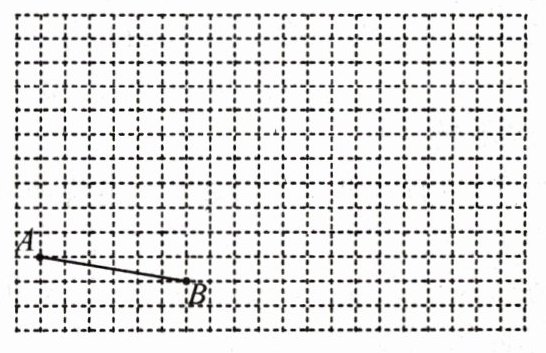
15. (8分)如图,方格纸上每个小正方形的面积为1.
(1)在方格纸上,以线段AB为边画正方形并计算所画正方形的面积.
(2)你能在图上画出面积依次为5,17的正方形吗?
(1)在方格纸上,以线段AB为边画正方形并计算所画正方形的面积.
(2)你能在图上画出面积依次为5,17的正方形吗?

答案:
解:
(1) 正方形 $A B C D$ 图略. $\because A B^{2}=1^{2}+6^{2}=37, \therefore$ 正方形 $A B C D$ 的面积为 37.
(2) 能. 图略, 正方形 $E F G H$, 正方形 $K L M N$ 即为所求.
(1) 正方形 $A B C D$ 图略. $\because A B^{2}=1^{2}+6^{2}=37, \therefore$ 正方形 $A B C D$ 的面积为 37.
(2) 能. 图略, 正方形 $E F G H$, 正方形 $K L M N$ 即为所求.
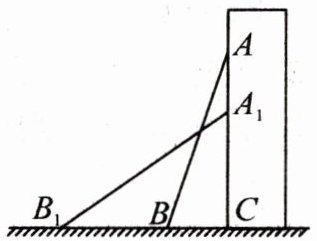
16. (10分)如图,一只小猫沿着斜靠在墙角的木板AB往上爬,木板底端距离墙角0.7 m,当小猫从木板底部爬到顶端A时,木板底端向墙外滑动了1.3 m,木板顶端向下滑动了0.9 m.
(1)根据题意,得$BC= $____m,$BB_{1}= $____m,$AA_{1}= $____m.
(2)求$A_{1}C$的长和这块木板的长.
(1)根据题意,得$BC= $____m,$BB_{1}= $____m,$AA_{1}= $____m.
(2)求$A_{1}C$的长和这块木板的长.

答案:
解:
(1) 0.7 1.3 0.9
(2) 设 $A_{1} C=x \mathrm{~m}$. 在 $\mathrm{Rt} \triangle A B C$ 和 $\mathrm{Rt} \triangle A_{1} B_{1} C$ 中, $A B^{2}=A C^{2}+B C^{2}, A_{1} B_{1}^{2}=A_{1} C^{2}+B_{1} C^{2}, \because A B=$ $A_{1} B_{1}, \therefore(0.9+x)^{2}+0.7^{2}=x^{2}+(1.3+0.7)^{2}$, 解得 $x=1.5$. $\therefore A B^{2}=B C^{2}+A C^{2}=0.7^{2}+(0.9+1.5)^{2}=6.25. \therefore A B=$ $2.5 \mathrm{~m}$. 答: $A_{1} C$ 的长是 $1.5 \mathrm{~m}$, 木板的长是 $2.5 \mathrm{~m}$.
(1) 0.7 1.3 0.9
(2) 设 $A_{1} C=x \mathrm{~m}$. 在 $\mathrm{Rt} \triangle A B C$ 和 $\mathrm{Rt} \triangle A_{1} B_{1} C$ 中, $A B^{2}=A C^{2}+B C^{2}, A_{1} B_{1}^{2}=A_{1} C^{2}+B_{1} C^{2}, \because A B=$ $A_{1} B_{1}, \therefore(0.9+x)^{2}+0.7^{2}=x^{2}+(1.3+0.7)^{2}$, 解得 $x=1.5$. $\therefore A B^{2}=B C^{2}+A C^{2}=0.7^{2}+(0.9+1.5)^{2}=6.25. \therefore A B=$ $2.5 \mathrm{~m}$. 答: $A_{1} C$ 的长是 $1.5 \mathrm{~m}$, 木板的长是 $2.5 \mathrm{~m}$.
17. (12分)如图,在$Rt△ABC$中,$∠ACB= 90^{\circ },AB= 5cm,AC= 3cm$,动点P从点B出发沿射线BC以1 cm/s的速度移动,设运动的时间为t s.
(1)求边BC的长.
(2)当$△ABP$为直角三角形时,求t的值.
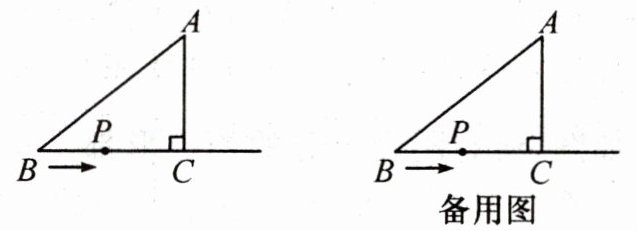
(1)求边BC的长.
(2)当$△ABP$为直角三角形时,求t的值.
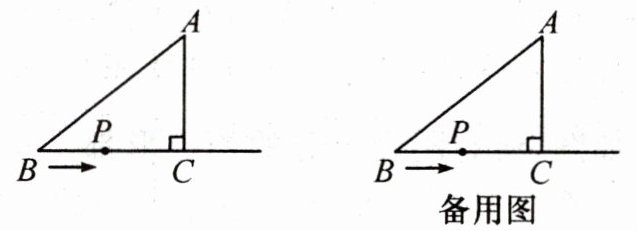
答案:
解:
(1) 在 $\mathrm{Rt} \triangle A B C$ 中, 由勾股定理, 得 $B C^{2}=A B^{2}-A C^{2}=5^{2}$ $-3^{2}=16, \therefore B C=4 \mathrm{~cm}$.
(2) 由题意, 得 $B P=t \mathrm{~cm}$, 分两种情况讨论:
(1) 当 $\angle A P B=90^{\circ}$ 时, 点 $P$ 与点 $C$ 重合, $\therefore B P=B C=$ $4 \mathrm{~cm} . \therefore t=4$;
(2) 当 $\angle B A P=90^{\circ}$ 时, 则 $C P=(t-4) \mathrm{cm}, \angle A C P$ $=90^{\circ}$, 在 $\mathrm{Rt} \triangle A C P$ 中, 由勾股定理, 得 $A P^{2}=A C^{2}+C P^{2}$, 在 $\mathrm{Rt} \triangle A B P$ 中, 由勾股定理, 得 $A P^{2}=B P^{2}-A B^{2}, \therefore A C^{2}+C P^{2}$ $=B P^{2}-A B^{2}$, 即 $3^{2}+(t-4)^{2}=t^{2}-5^{2}$, 解得 $t=\frac{25}{4}$. 综上所述,当 $\triangle A B P$ 为直角三角形时, $t$ 的值为 4 或 $\frac{25}{4}$.
(1) 在 $\mathrm{Rt} \triangle A B C$ 中, 由勾股定理, 得 $B C^{2}=A B^{2}-A C^{2}=5^{2}$ $-3^{2}=16, \therefore B C=4 \mathrm{~cm}$.
(2) 由题意, 得 $B P=t \mathrm{~cm}$, 分两种情况讨论:
(1) 当 $\angle A P B=90^{\circ}$ 时, 点 $P$ 与点 $C$ 重合, $\therefore B P=B C=$ $4 \mathrm{~cm} . \therefore t=4$;
(2) 当 $\angle B A P=90^{\circ}$ 时, 则 $C P=(t-4) \mathrm{cm}, \angle A C P$ $=90^{\circ}$, 在 $\mathrm{Rt} \triangle A C P$ 中, 由勾股定理, 得 $A P^{2}=A C^{2}+C P^{2}$, 在 $\mathrm{Rt} \triangle A B P$ 中, 由勾股定理, 得 $A P^{2}=B P^{2}-A B^{2}, \therefore A C^{2}+C P^{2}$ $=B P^{2}-A B^{2}$, 即 $3^{2}+(t-4)^{2}=t^{2}-5^{2}$, 解得 $t=\frac{25}{4}$. 综上所述,当 $\triangle A B P$ 为直角三角形时, $t$ 的值为 4 或 $\frac{25}{4}$.
查看更多完整答案,请扫码查看


