《2025年53精准练七年级数学下册北师大版山西专版》

11. 如图，点P在BC上，AB⊥BC于点B，DC⊥BC于点C，△ABP≌△PCD，其中BP = CD，则下列结论中错误的是 （ ）


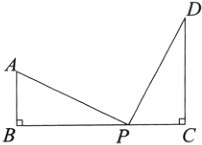
A. ∠APB = ∠D
B. ∠A + ∠CPD = 90°
C. AP = PD
D. AB = PC

答案： B

12. 如图，△ABC≌△ADE，线段BC的延长线过点E，与线段AD交于点F，∠AED = 108°，∠CAD = 12°，∠B = 48°，则∠DEF = （ ）


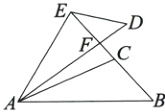
A. 28°
B. 36°
C. 38°
D. 42°

答案： B

13. [2023吕梁临县期末]如图，△ABE≌△ADC≌△ABC，若∠1 = 150°，则∠α的度数为_______.

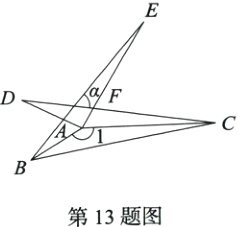
答案： 60°

14. 三个全等三角形按图中的形式摆放，则∠1 + ∠2 + ∠3的度数是__________.

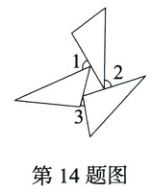
答案：
180°
详解：如图

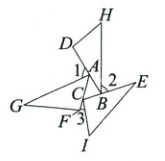
根据题意可知△AFG≌△HDB≌△ICE，
所以∠HBD = ∠AGF，
∠ICE = ∠AFG，
因为∠1 + ∠GAF + ∠CAB = 180°，
∠2 + ∠HBD + ∠ABC = 180°，
∠3 + ∠ICE + ∠BCA = 180°，
所以∠1 + ∠2 + ∠3 = 540° - ∠GAF - ∠CAB - ∠HBD - ∠ABC - ∠ICE - ∠BCA
= 540° - (∠GAF + ∠AGF + ∠AFG) - (∠CAB + ∠ABC + ∠BCA) = 180°.

15. 如图，△ACE≌△AFB，CE与AB、BF分别交于点D、M.已知AE⊥AB，在图中找出其他互相垂直的直线，并说明理由.

答案： 解：①AC⊥AF.理由如下：
因为AE⊥AB，
所以∠EAB = 90°.
因为△AFB≌△ACE，
所以∠BAF = ∠EAC，
所以∠BAF - ∠BAC = ∠EAC - ∠BAC，
所以∠CAF = ∠EAB = 90°，
所以AC⊥AF.
②EC⊥BF.理由如下：
因为AE⊥AB，
所以∠EAB = 90°，
所以∠E + ∠EDA = 90°.
因为△ACE≌△AFB，
所以∠E = ∠B，
又因为∠EDA = ∠BDM，
所以∠B + ∠BDM = 90°，
所以∠BMD = 90°，
所以EC⊥BF.

16. [分类讨论·2024太原小店区月考]如图①，在Rt△ABC中，∠C = 90°，BC = 9 cm，AC = 12 cm，AB = 15 cm，现有一动点P，从点A出发，沿着三角形的边AC→CB→BA运动，回到点A停止，速度为3 cm/s，设运动时间为t s.

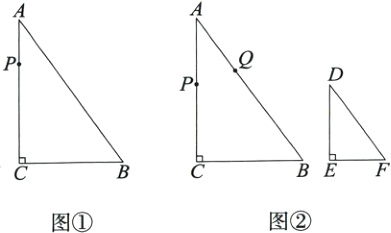
(1)如图①，当t =________s时，△APC的面积等于△ABC面积的一半.
(2)如图②，在△DEF中，∠E = 90°，DE = 4 cm，DF = 5 cm，∠D = ∠A.在△ABC的边上，另外有一个动点Q，与点P同时从点A出发，沿着边AB→BC→CA运动，回到点A停止.若在两点运动过程中的某一时刻，恰好△APQ≌△DEF，求点Q的运动速度.

答案：
解：
(1)$\frac{11}{2}$或$\frac{19}{2}$.
(2)因为△APQ≌△DEF，
所以AP = DE = 4cm，
AQ = DF = 5cm.
当点P在AC上时，如图①所示，
因为AP = 4cm，AQ = 5cm，
所以点Q运动的速度为5÷(4÷3) = $\frac{15}{4}$(cm/s)；

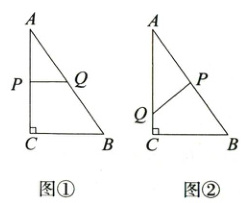
当点P在AB上时，如图②所示，
因为AP = 4cm，AQ = 5cm，
所以点P运动的距离为9 + 12 + 15 - 4 = 32(cm)，
点Q运动的距离为15 + 9 + 12 - 5 = 31(cm)，
所以点Q运动的速度为31÷(32÷3) = $\frac{93}{32}$(cm/s).
故点Q的运动速度为$\frac{15}{4}$cm/s或$\frac{93}{32}$cm/s.