《2025年53精准练七年级数学下册北师大版山西专版》

1.计算：$(a\cdot a^{3})^{2}=a^{2}\cdot (a^{3})^{2}=a^{2}\cdot a^{6}=a^{8}$，其中，第一步运算的依据是（ ）
A. 同底数幂的乘法法则
B. 幂的乘方法则
C. 乘法分配律
D. 积的乘方法则

答案： D

2.下列计算正确的是（ ）
A. $(xy^{2})^{2}=xy^{4}$
B. $(3xy)^{3}=9x^{3}y$
C. $(-2a^{2})^{2}=-4a^{4}$
D. $(-3ab^{2})^{2}=9a^{2}b^{4}$

答案： D

3.[2024太原晋源区月考]计算$\left(-\frac{1}{2}xy^{2}\right)^{3}$的结果是（ ）
A. $\frac{1}{6}x^{3}y^{5}$
B. $-\frac{1}{8}x^{3}y^{6}$
C. $\frac{1}{6}x^{3}y^{6}$
D. $-\frac{1}{8}x^{3}y^{5}$

答案： B

4.一个正方体的棱长为$2\times10^{2}\text{ mm}$，则它的体积是（ ）
A. $8\times10^{2}\text{ mm}^{3}$
B. $6\times10^{5}\text{ mm}^{3}$
C. $8\times10^{6}\text{ mm}^{3}$
D. $6\times10^{6}\text{ mm}^{3}$

答案： C

5.计算：
(1)$\left(\frac{2}{5}a^{4}\right)^{3}$；
(2)$-(3m^{2}n^{3})^{2}$；
(3)$(7a^{2}b)^{n}$；
(4)$(-4x^{m}y^{2n})^{3}$.

答案： 解：
(1)原式$=(\frac{2}{5})^{3}\cdot(a^{4})^{3}=\frac{8}{125}a^{12}$.
(2)原式$=-3^{2}\cdot(m^{2})^{2}\cdot(n^{3})^{2}=-9m^{4}n^{6}$.
(3)原式$=7^{n}\cdot(a^{2})^{n}\cdot b^{n}=7^{n}a^{2n}b^{n}$.
(4)原式$=(-4)^{3}\cdot(x^{m})^{3}\cdot(y^{2n})^{3}=-64x^{3m}y^{6n}$.

6.填空：$8x^{3}=(\ \ \ \ )^{3}$；$0.0169a^{4}b^{6}=(\ \ \ \ )^{2}$；$\frac{196}{81}m^{2}n^{4}=(\ \ \ \ )^{2}$.

答案： $2x$; $\pm0.13a^{2}b^{3}$; $\pm\frac{14}{9}mn^{2}$

7. $0.2^{4}\times4^{4}\times12.5^{4}=$__________.

答案： 10000

8.计算$\left(-\frac{12}{13}\right)^{2025}\times\left(\frac{13}{12}\right)^{2025}$的结果是__________.

答案： -1

9.已知$a^{2m}b^{m}=10$，$18^{m}=10$，若$b = 2$，则$a=$_____.

答案： $\pm3$

10.下列各图中，能直观解释“$(3a)^{2}=9a^{2}$”的是（ ）

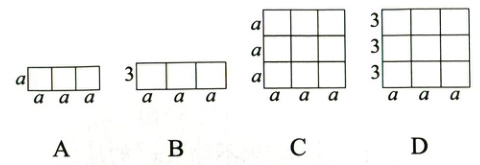
答案： C

11.若$(3a^{m}b^{m - n})^{2}=9a^{4}b^{8}$成立，则（ ）
A. $m = 2$，$n = - 2$
B. $m = - 2$，$n = - 2$
C. $m = - 2$，$n = 2$
D. $m = 2$，$n = 2$

答案： A

12.计算：
(1)$(-5ab^{4})^{2}\cdot ab^{4}+(2ab^{4})^{3}$；
(2)$(3x^{12})^{2}+(-2x^{8})^{3}+(x^{4})^{5}\cdot x^{4}$.

答案： 解：
(1)原式$=25\cdot a^{2}\cdot b^{8}\cdot ab^{4}+8a^{3}b^{12}=25a^{3}b^{12}+8a^{3}b^{12}=33a^{3}b^{12}$.
(2)原式$=9x^{24}-8x^{24}+x^{24}=2x^{24}$.

13.规定$a*b = ab - 1$，如：$2*1 = 2\times1 - 1 = 1$.
(1)若$4^{2}*4^{x - 1}=63$，求$x$的值；
(2)求$\left(\frac{4}{3}\right)^{2024}*(-0.75)^{2025}$的值.

答案： 解：
(1)因为$4^{2}\times4^{x - 1}=64$，
所以$4^{2 + x - 1}=64 = 4^{3}$，
所以$1 + x = 3$，即$x = 2$.
(2)由题得$(\frac{4}{3})^{2024}\times(-0.75)^{2025}$
$=(\frac{4}{3})^{2024}\times(-0.75)^{2024}\times(-0.75)$
$=[\frac{4}{3}\times(-0.75)]^{2024}\times(-0.75)$
$=(-1)^{2024}\times(-0.75)$
$=-0.75$.