《2025年核心素养天天练四年级数学下册北师大版》

1. 选一选。
（1）下面6种图形中能密铺的有(　　　)个。

A. 4
B. 5
C. 6
（2）能够铺满地面的正多边形的组合可能是(　　　)。（多选）
A. 正三角形与正方形
B. 正五边形与正十边形
C. 正六边形与正三角形

答案：
(1)A　解析:平行四边形、三角形、梯形和由4个正方形组成的图形都可以密铺，所以能密铺的图形有4个。
(2)ABC　解析:两个正方形和三个正三角形绕一点可以拼成一个周角;两个正五边形与一个正十边形绕一点可以拼成一个周角;一个正六边形和四个正三角形绕一点可以拼成一个周角，两个正六边形和两个正三角形绕一点可以拼成一个周角。

2. 仔细观察下面的图案，你知道它们分别是由什么图形密铺而成的吗？在下面的括号内画出来。

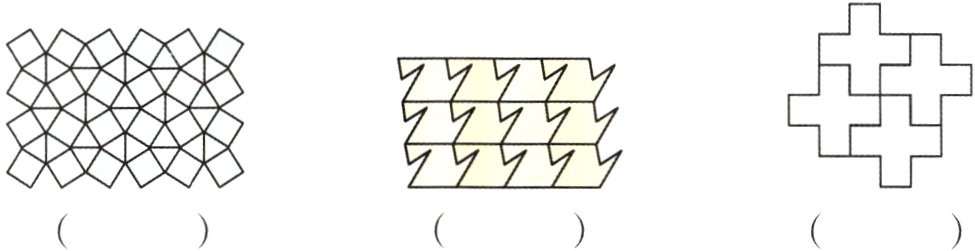
答案：

3. 在一个工厂的废料堆里，堆放着大量不规则的四边形木料（如图），这四块木料的大小和形状是一样的。如果把它们做成比较规则的形状，必须锯掉一些边角，就要浪费很多木料。有人建议用这些木料来铺地板，你认为这些木料能密铺吗？为什么？

答案： 能，因为四边形的内角和是360°，按如图所示的拼法拼接，就能填满这个平面，而且无缝隙。因此，凡是有着同样大小、同样形状的任意四边形木块，都可用来拼地板。

4. 用蓝、白两种颜色的正六边形地砖按如图所示的规律拼成若干个图案。
（1）第四个图案中有(　　)块白色地砖。
（2）第n个图案中有(　　)块白色地砖。

答案：
(1)18　解析:第1个图案有6块白色地砖，以后每多组成一个图案，就要增加4块白色地砖，所以第四个图案在第1个图案的基础上增加了3个4块白色地砖。
(2)4n + 2　解析:把第1个图案看成是(4 + 2)块白色地砖，则图案数与白色地砖数的规律是图案数×4 + 2 = 白色地砖数，所以第n个图案的白色地砖数为(4n + 2)块。

8.3 - 3.2 =
3.14 + 2.36 =
2.38 + 2.4 =
6.78 - 2.36 =
5.12 + 2.34 =
6.89 - 0.88 =
3.26×10 =
0.28×100 =

答案： 5.1　5.5　4.78　4.42　7.46　6.01　32.6　28