《2025年核心素养天天练四年级数学下册北师大版》

1. 如右图，三角形ABC是一个( )三角形，它的内角和是( )°。

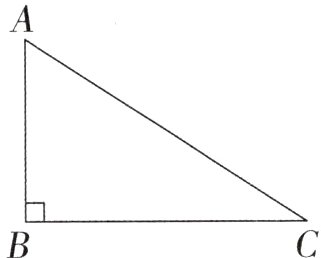
答案： 直角 180

2. 一个三角形的两角之和是83°，这个三角形是( )三角形。

答案： 钝角 解析：因为三角形的两角之和是83°，所以另一个角为97°，这个三角形是钝角三角形。

3. 一个四边形，如果只有一组对边平行，它是( )；如果有两组对边分别平行，它是( )。

答案： 梯形 平行四边形 解析：只有一组对边平行的四边形是梯形，两组对边分别平行的四边形是平行四边形。

4. 一个三角形中最大的一个内角是85°，这是一个( )三角形。

答案： 锐角 解析：因为这个三角形最大的内角是85°，其他两个内角都小于85°，所以这是锐角三角形。

5. 一个三角形中有一个角是45°，另一个角是它的2倍，第三个角的度数是( )，这是一个( )三角形。

答案： 45° 等腰直角 解析：这个三角形另一个角是45°的2倍，就是90°，所以第三个角也是45°，这是一个等腰直角三角形。

6. 根据同学们的描述，这个三角形的周长是( )厘米。

答案： 18

二、判断。(每题2分，共10分)
1. 梯形是特殊的四边形。( )
2. 有三条线段分别是3厘米、3厘米和6厘米，可以围成一个等腰三角形。( )
3. 长方形和平行四边形都是轴对称图形。( )
4. 用四根木条钉成一个平行四边形，用手去拉它，这个平行四边形可以变成一个长方形。( )
5. 平行四边形的对边分别平行，但不相等。( )

答案： √ 解析：梯形是四边形，且只有一组对边平行，所以是特殊的四边形。
@@× 解析：因为3 + 3 = 6（厘米），而另一条边也是6厘米，所以不能围成等腰三角形。
@@× 解析：长方形是轴对称图形，平行四边形不是轴对称图形。
@@√ 解析：当把平行四边形的四个角拉成直角时，它就变成了长方形。
@@× 解析：平行四边形的对边分别平行且相等。

1. 在直角三角形中，一个锐角是60°，另一个锐角是( )。
A. 30° B. 45° C. 60°

答案： A 解析：直角三角形中一个锐角是60°，另一个锐角就是180° - 90° - 60° = 30°。

2. 三角形的三个内角中，至少有( )。
A. 两个锐角 B. 一个锐角和一个直角 C. 一个锐角

答案： A 解析：180°减去一个直角或一个钝角，都小于90°，所以一个三角形中至少有两个锐角。

3. 已知一个角是12°，用放大2倍的放大镜看，这个角是( )。
A. 12° B. 24° C. 6°

答案： A 解析：角的大小与角的张口大小有关，与边的粗细和长短无关。