第95页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
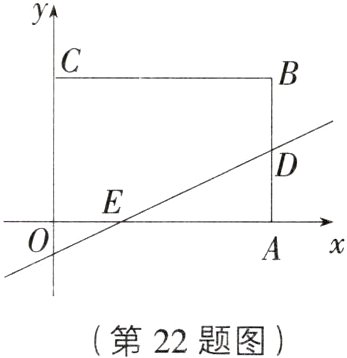
22. (7分)如图,矩形OABC顶点A(8,0),C(0,6),直线$y = kx - 1$分别交BA,OA于点D,E,且D为BA中点.
(1)求k的值及此时△EAD的面积;
(2)现向矩形内随机投飞镖,求飞镖落在△EAD内的概率.(若投在边框上则重投)
(1)求k的值及此时△EAD的面积;
(2)现向矩形内随机投飞镖,求飞镖落在△EAD内的概率.(若投在边框上则重投)

答案:
[解析]
(1)
∵矩形OABC顶点A(8,0),C(0,6),
∴B(8,6),
∵D为BA中点,
∴D(8,3),AD=3,把点D(8,3)代入y=kx−1得k=$\frac{1}{2}$;令y=0,得x=2,
∴E(2,0),
∴OE=2,AE=6,
∴S_{△EAD}=$\frac{1}{2}$×6×3=9;
(2)由
(1)得S_{矩形OABC}=6×8=48,
∴P=$\frac{9}{48}$=$\frac{3}{16}$
(1)
∵矩形OABC顶点A(8,0),C(0,6),
∴B(8,6),
∵D为BA中点,
∴D(8,3),AD=3,把点D(8,3)代入y=kx−1得k=$\frac{1}{2}$;令y=0,得x=2,
∴E(2,0),
∴OE=2,AE=6,
∴S_{△EAD}=$\frac{1}{2}$×6×3=9;
(2)由
(1)得S_{矩形OABC}=6×8=48,
∴P=$\frac{9}{48}$=$\frac{3}{16}$
23. (7分)“品中华诗词,寻文化基因.”某校举办了第二届“中华诗词大赛”,将该校九年级参加竞赛的学生成绩统计后,绘制了如下不完整的频数分布统计表与频数分布直方图.
频数分布统计表

频数分布直方图

请观察图表,解答下列问题:
(1)表中a = ______,m = ______;
(2)补全频数分布直方图;
(3)D组的4名学生中,有1名男生和3名女生.现从中随机抽取2名学生参加市级竞赛,则抽取的2名学生恰好是一名男生和一名女生的概率.
频数分布统计表

频数分布直方图

请观察图表,解答下列问题:
(1)表中a = ______,m = ______;
(2)补全频数分布直方图;
(3)D组的4名学生中,有1名男生和3名女生.现从中随机抽取2名学生参加市级竞赛,则抽取的2名学生恰好是一名男生和一名女生的概率.
答案:
[解析]
(1)12 40
提示:
∵被调查的总人数为8÷20%=40,a=40×30%=12,m%=$\frac{16}{40}$×100%=40%,即m=40;
(2)补全图形如图: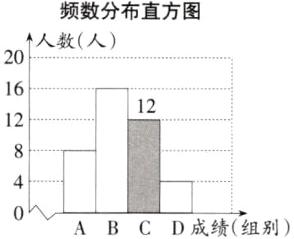
(3)画树形图如下: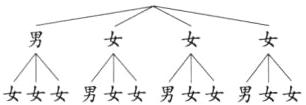
∵共有12种等可能的结果,选中1 名男生和1名女生的结果有6种,
∴抽取的2名学生恰好是一名男生和一名女生的概率为$\frac{6}{12}$=$\frac{1}{2}$
[解析]
(1)12 40
提示:
∵被调查的总人数为8÷20%=40,a=40×30%=12,m%=$\frac{16}{40}$×100%=40%,即m=40;
(2)补全图形如图:

(3)画树形图如下:

∵共有12种等可能的结果,选中1 名男生和1名女生的结果有6种,
∴抽取的2名学生恰好是一名男生和一名女生的概率为$\frac{6}{12}$=$\frac{1}{2}$
24. (8分)在一个不透明的口袋里装有分别标注2,4,6的3个小球(小球除数字不同外,其余都相同),另有3张背面完全一样、正面分别写有数字6,7,8的卡片.现从口袋中任意摸出一个小球,再从这3张背面朝上的卡片中任意摸出一张卡片.
(1)请你用列表的方法,表示出所有可能出现的结果;
(2)小红和小莉做游戏,制定了如下两个游戏规则:
规则1:若两次摸出的数字,至少有一次是“6”,小红赢;否则,小莉赢.
规则2:若摸出的卡片上的数字是球上数字的整数倍时,小红赢;否则,小莉赢.
小红要想在游戏中获胜,她会选择哪一种规则,并说明理由.
(1)请你用列表的方法,表示出所有可能出现的结果;
(2)小红和小莉做游戏,制定了如下两个游戏规则:
规则1:若两次摸出的数字,至少有一次是“6”,小红赢;否则,小莉赢.
规则2:若摸出的卡片上的数字是球上数字的整数倍时,小红赢;否则,小莉赢.
小红要想在游戏中获胜,她会选择哪一种规则,并说明理由.
答案:
[解析]
(1)列表如下:
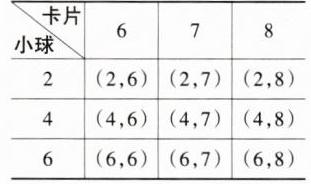
共有9种等可能的情况,分别是(2,6),(2,7),(2,8),(4,6),(4,7),(4,8),(6,6),(6,7),(6,8);
(2)从图表可知,至少有一次是“6”的情况有5种,所以小红赢的概率是P=$\frac{5}{9}$,小莉赢的概率是P=1−$\frac{5}{9}$=$\frac{4}{9}$,
∵$\frac{5}{9}$>$\frac{4}{9}$,
∴规则1小红获胜的概率大;
卡片上的数字是球上数字的整数倍的有(2,6),(2,8),(4,8),(6,6)共4种情况,所以小红赢的概率是P=$\frac{4}{9}$,小莉赢的概率是P=1−$\frac{4}{9}$=$\frac{5}{9}$,
∵$\frac{5}{9}$>$\frac{4}{9}$,
∴规则2小莉获胜的概率大,
∴小红要想在游戏中获胜,她应该选择规则1.
[解析]
(1)列表如下:

共有9种等可能的情况,分别是(2,6),(2,7),(2,8),(4,6),(4,7),(4,8),(6,6),(6,7),(6,8);
(2)从图表可知,至少有一次是“6”的情况有5种,所以小红赢的概率是P=$\frac{5}{9}$,小莉赢的概率是P=1−$\frac{5}{9}$=$\frac{4}{9}$,
∵$\frac{5}{9}$>$\frac{4}{9}$,
∴规则1小红获胜的概率大;
卡片上的数字是球上数字的整数倍的有(2,6),(2,8),(4,8),(6,6)共4种情况,所以小红赢的概率是P=$\frac{4}{9}$,小莉赢的概率是P=1−$\frac{4}{9}$=$\frac{5}{9}$,
∵$\frac{5}{9}$>$\frac{4}{9}$,
∴规则2小莉获胜的概率大,
∴小红要想在游戏中获胜,她应该选择规则1.
查看更多完整答案,请扫码查看


