《2025年考点集训与满分备考九年级数学下册冀教版》

11. 已知⊙O的半径为5，直线AB与⊙O有公共点，则圆心O到直线AB的距离不可能为（ ）
A. 5
B. 5.5
C. 4.5
D. 1

答案： B [解析]
∵⊙O的半径为5，直线AB与⊙O有公共点，
∴圆心O到直线AB的距离d≤5.

12. 如图，已知⊙O的半径为6，点O到某条直线的距离为8，则这条直线可以是（ ）

A. l₁
B. l₂
C. l₃
D. l₄

答案： B [解析]
∵⊙O的半径为6，点O到某条直线的距离为8，
∴这条直线与圆相离.

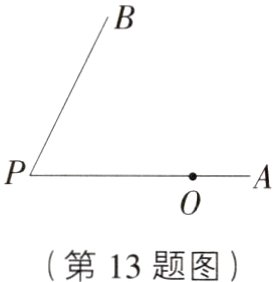
13. 易错题 如图，∠APB = 60°，O为PA上一点，且PO = 4，以点O为圆心，半径为3√3的圆与PB的位置关系是（ ）

A. 相离
B. 相切
C. 相交
D. 相切、相离或相交

答案：
C [解析]如图，过点O作OC⊥PB于点C，
∵∠APB = 60°，OP = 4，
∴OC = √3/2×OP = 2√3＜3√3，
∴半径为3√3的圆与PB的位置关系是相交.

14. 较难题 如图，在△ABC中，∠C = 40°，∠A = 60°.以点B为圆心，适当长为半径作弧，分别交AB，BC于点D，E；分别以点D，E为圆心，大于1/2DE长为半径作弧，两弧交于点F；作射线BF，交AC于点P，过点P作PM⊥AB于点M；以点P为圆心，PM的长为半径作⊙P.则下列结论中，错误的是（ ）

A. ∠PBA = 40°
B. PC = PB
C. PM = MB
D. ⊙P与△ABC有4个公共点

答案： C [解析]
∵∠C = 40°，∠A = 60°，
∴∠ABC = 80°，由题意得，BP平分∠ABC，
∴∠ABP = 1/2×∠ABC = 40°，故选项A正确；
∵∠PBC = ∠PBA = 1/2×∠ABC = 40°，
∴∠C = ∠PBC，
∴PC = PB，故选项B正确；
∵PM⊥AB，
∴∠BMP = 90°，
∴∠BPM = 50°，
∴∠BPM≠∠MBP，
∴PM≠BM，故选项C错误；
∵点P在∠ABC的平分线上，
∴点P到AB和BC的距离 = PM = ⊙P的半径，AB，BC与⊙P相切，
∵PA＞PM，PC＞PM，
∴⊙P与AC相交，
∴⊙P与△ABC有4个公共点，故选项D正确.

15. 已知⊙O的半径r = 2，圆心O到直线l的距离d是方程x² - 5x + 6 = 0的解，则直线l与⊙O的位置关系是 ______.

答案： 相切或相离 [解析]x² - 5x + 6 = 0，(x - 3)(x - 2) = 0，x = 3或2，当d = 3时，则d＞r，
∴直线l与⊙O的位置关系是相离；当d = 2时，则d = r，
∴直线l与⊙O的位置关系是相切；
∴直线l与⊙O的位置关系是相切或相离.

16. 推理能力 如图，在平面直角坐标系中，A(0,4)，B(4,4)，C(6,2)，则经过A，B，C三点的圆弧所在圆的圆心M的坐标为(2,0)；若点D坐标为(8,-2)，连接CD，直线CD与⊙M的位置关系是 ______.

答案：
相切 [解析]如图，连接MC，MD，MA，MC² = 4² + 2² = 20，CD² = 4² + 2² = 20，MD² = 6² + 2² = 40，MD² = MC² + CD²，
∴∠MCD = 90°，MC⊥CD，又
∵MA² = 4² + 2² = 20，
∴MC = MA，
∴直线CD与⊙M相切.

17. 推理能力 如图，已知△AOB中，OA = OB，∠AOB = 120°，以点O为圆心，1/2OA长为半径作圆分别交OA，OB于点C，D，弦MN//AB.
(1)判断直线AB与⊙O的位置关系并说明理由；
(2)求证：⌢MC = ⌢ND.

答案：
[解析]
(1)相切，理由：如图，过点O作OE⊥AB，垂足为E，
∵△AOB中，OA = OB，∠AOB = 120°，
∴∠A = ∠B = 1/2×(180° - 120°) = 30°，在Rt△AOE中，∠A = 30°，
∴OE = 1/2×OA，又
∵OC = 1/2×OA，
∴OE = OC，
∴AB与⊙O相切；

(2)如图，连接CD，
∵OC = OD，∠AOB = 120°，
∴∠OCD = ∠ODC = 30°，
∴CD//AB，
∵MN//AB，
∴MN//CD，
∴MC弧 = ND弧.

18. 动点问题 如图，在矩形ABCD中，E为AB边的中点，F为边AD上的动点，过点F作EF的垂线交DC于点H，以EF为直径作半圆O.
(1)填空：①点A与⊙O的位置关系是 ____；
②当⌢AE = ⌢AF 时，tan∠AEF的值是 ______；
③当点F与点A重合时，⊙O与矩形ABCD的边AD的位置关系是 __________；
(2)当△EFH的顶点F是边AD的中点时，若AB = 8，AD = 6，求线段DH的长.

答案：
[解析]
(1)①点A在⊙O上
提示：如图1，连接OA，
∵四边形ABCD是矩形，
∴∠EAF = 90°，
∵EF为半圆O的直径，
∴O为EF的中点，
∴OA = OE = OF，
∴点A在⊙O上；

②1 提示：如图2，
∵AE弧 = AF弧，
∴∠AEF = ∠AFE，
∵∠EAF = 90°，
∴∠AEF = 45°，
∴tan∠AEF = 1；
③相切 提示：如图3，当点F与点A重合时，H与D重合，
∴OF⊥FH，圆心O到直线AD的距离OA = OF，
∴AD与⊙O相切；

(2)如图4，
∵E为AB边的中点，
∴AE = 1/2×AB = 4，
∵F是AD边的中点，AF = DF = 1/2×AD = 3，
∵EF⊥FH，
∴∠EFH = 90°，在矩形ABCD中，∠A = ∠D = 90°，
∴∠AEF + ∠AFE = 90°，∠AFE + ∠DFH = 90°，
∴∠AEF = ∠DFH，
∴△AEF∽△DFH，
∴AE/DF = AF/DH，即4/3 = 3/DH，DH = 9/4.