《2025年考点集训与满分备考九年级数学下册冀教版》

9. 某小组对某品种小麦发芽情况进行测试，在测试基本情况相同的条件下，得到如下数据：

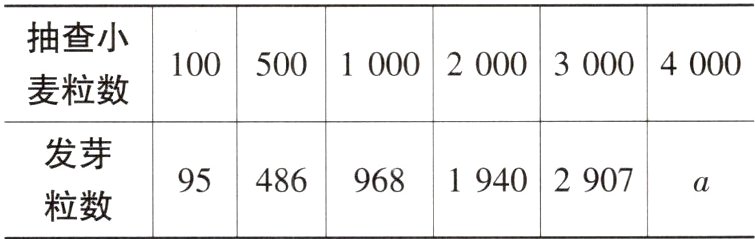
则a的值最有可能是 （ ）
A. 3680
B. 3720
C. 3880
D. 3960

答案： C ［解析］
∵95÷100 = 0.95，486÷500 = 0.972，968÷1 000 = 0.968，1 940÷2 000 = 0.97，2 907÷3 000 = 0.969，
∴可估计该品种小麦发芽的概率为0.97，而3 680÷4 000 = 0.92，3 720÷4 000 = 0.93，3 880÷4 000 = 0.97，3 960÷4 000 = 0.99.
∴a的值最有可能是3 880.

10. 小明和同学做“抛掷质地均匀的硬币试验”获得的数据如下表：

若抛掷硬币的次数为1000，则“正面朝上”的频数最接近 （ ）
A. 20
B. 300
C. 500
D. 800

答案： C ［解析］观察表格发现：随着试验次数的增加，正面朝上的频率逐渐稳定到0.5附近，所以抛掷硬币的次数为1 000，则“正面朝上”的频数最接近1 000×0.5 = 500(次).

11. 易错题下列说法正确的是 （ ）
A. 某活动的中奖概率是5%，那么抽100次奖一定有5次中奖
B. 某次试验投掷次数是500，计算机记录“钉尖向上”的次数是308，则该次试验“钉尖向上”的频率是0.616
C. 当试验次数很大时，概率稳定在频率附近
D. 试验得到的频率与概率不可能相等

答案： B ［解析］A.某活动的中奖概率是5%，那么抽100次奖可能有5次中奖，此选项说法错误；B.某次试验投掷次数是500，计算机记录“钉尖向上”的次数是308，则该次试验“钉尖向上”的频率是0.616，此选项说法正确；C.当试验次数很大时，频率稳定在概率附近，此选项说法错误；D.试验得到的频率与概率可能相等，此选项说法错误.

12. 在一个不透明的布袋中装有52个白球和若干个黑球，除颜色外其他都相同，小强每次摸出一个球记录下颜色后并放回，通过多次试验后发现，摸到黑球的频率稳定在0.2左右，则布袋中黑球的个数可能是 （ ）
A. 11
B. 13
C. 24
D. 30

答案： B ［解析］设袋中有黑球x个，由题意得$\frac{x}{52 + x}$ = 0.2，解得x = 13，经检验x = 13是原方程的解，则布袋中黑球可能有13个.

13. 数据观念某小组在“用频率估计概率”的试验中，统计了某种结果出现的频率，绘制了如图所示的折线统计图，那么符合这一结果的试验最有可能的是 （ ）

A. 掷一枚质地均匀的硬币，落地时结果是“正面向上”
B. 掷一个质地均匀的正六面体骰子，落地时朝上的面点数是6
C. 在“石头、剪刀、布”的游戏中，小明随机出的是“剪刀”
D. 袋子中有1个红球和2个黄球，只有颜色上的区别，从中随机取出一个球是黄球

答案： B ［解析］A.掷一枚质地均匀的硬币，落地时结果是“正面向上”的概率为$\frac{1}{2}$，不符合题意；B.掷一个质地均匀的正六面体骰子，落地时面朝上的点数是6的概率为$\frac{1}{6}$，符合题意；C.在“石头、剪刀、布”的游戏中，小明随机出的是“剪刀”的概率为$\frac{1}{3}$，不符合题意；D.袋子中有1个红球和2个黄球，它们只有颜色上的区别，从中随机地取出一个球是黄球的概率为$\frac{2}{3}$，不符合题意.

14. 数形结合如图，在边长为3的正方形内有区域A（阴影部分所示），小梅同学用随机模拟的方法求区域A的面积，若每次在正方形内随机产生10000个点，并记录落在区域A内的点的个数，经过多次试验，计算出落在区域A内点的个数的平均值为6600个，则估计区域A的面积为________.

答案： 5.94 ［解析］
∵在正方形中随机产生了10 000个点，落在区域A内点的个数平均值为6 600个，
∴频率值趋于$\frac{6 600}{10 000}$ = 0.66，
∴估计落在区域A内概率为0.66，
∵边长为3的正方形的面积为9，
∴区域A的面积的估计值为0.66×9 = 5.94.