《2025年考点集训与满分备考九年级数学下册冀教版》

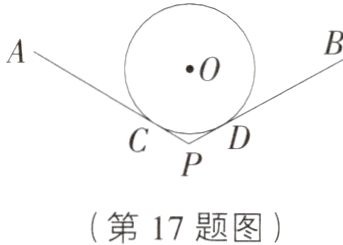
17. 传统文化 抖空竹在我国有着悠久的历史，是国家级的非物质文化遗产之一.如图，AC，BD分别与⊙O相切于点C，D，延长AC，BD交于点P.若∠P=120°，⊙O的半径为6 cm，则图中⌢CD的长为_____ cm.(结果保留π)

答案：
$2\pi$ [解析] 如图，连接 $OC$，$OD$，$OP$，
$\because AC$，$BD$ 分别与 $\odot O$ 相切于点 $C$，$D$，故 $\angle OCP=\angle ODP = 90^{\circ}$，由四边形内角和为 $360^{\circ}$ 可得，$\angle COD = 360^{\circ}-\angle OCP-\angle ODP-\angle CPD = 360^{\circ}-90^{\circ}-90^{\circ}-120^{\circ}=60^{\circ}$。
$\therefore \widehat{CD}$ 的长为 $\frac{n\pi r}{180}=\frac{60\times\pi\times6}{180}=2\pi(cm)$。

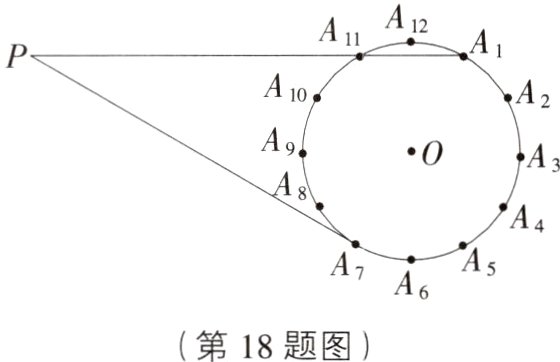
18. 如图，⊙O的半径为6，将该圆周12等分后得到表盘模型，其中整钟点为An(n为1~12的整数)，过点A7作⊙O的切线交A1A11的延长线于点P.
(1)通过计算比较直径和劣弧⌢A7A11哪个更长；
(2)连接A7A11，则A7A11和PA1有什么特殊位置关系? 请简要说明理由；
(3)求PA7的长.

答案：
[解析]
(1)由题意，$\angle A_{7}OA_{11}=120^{\circ}$，
$\therefore$ 劣弧 $\widehat{A_{7}A_{11}}$ 的长为 $\frac{120\pi\times6}{180}=4\pi＞12$，$\therefore$ 劣弧 $\widehat{A_{7}A_{11}}$ 比直径长；
(2)结论：$PA_{1}\perp A_{7}A_{11}$。理由：如图，连接 $A_{1}A_{7}$，$A_{7}A_{11}$，$OA_{11}$。$\because A_{1}A_{7}$ 是 $\odot O$ 的直径，$\therefore \angle A_{7}A_{11}A_{1}=90^{\circ}$，$\therefore PA_{1}\perp A_{7}A_{11}$；

(3)$\because PA_{7}$ 是 $\odot O$ 的切线，$\therefore PA_{7}\perp A_{1}A_{7}$，$\therefore \angle PA_{7}A_{1}=90^{\circ}$，易得 $\angle PA_{1}A_{7}=60^{\circ}$，$A_{1}A_{7}=12$，$\therefore PA_{7}=A_{1}A_{7}\cdot\tan60^{\circ}=12\sqrt{3}$。

19. 新情境·石磨 在古代，智慧的劳动人民已经会使用“石磨”，其原理为在磨盘的边缘连接一个固定长度的“连杆”，推动“连杆”带动磨盘转动，将粮食磨碎，物理学上称这种动力传输工具为“曲柄连杆机构”.
小明受此启发设计了一个“双连杆机构”，设计图如图1所示，两个固定长度的“连杆”AP，BP的连接点P在⊙O上，当点P在⊙O上转动时，带动点A，B分别在射线OM，ON上滑动，OM⊥ON.当AP与⊙O相切时，点B恰好落在⊙O上，如图2.
请仅就图2的情形解答下列问题.
(1)求证：∠PAO=2∠PBO；
(2)若⊙O的半径为5，AP=20/3 ，求BP的长.

答案：
[解析]
(1)如图 1，连接 $OP$，延长 $BO$ 与 $\odot O$ 交于点 $C$，则 $OP = OB = OC$，
$\because AP$ 与 $\odot O$ 相切于点 $P$，$\therefore \angle APO = 90^{\circ}$，$\therefore \angle PAO+\angle AOP = 90^{\circ}$，
$\because MO\perp CN$，$\therefore \angle AOP+\angle POC = 90^{\circ}$，
$\therefore \angle PAO=\angle POC$，
$\because OP = OB$，$\therefore \angle OPB=\angle PBO$，
$\therefore \angle POC=\angle OPB+\angle PBO = 2\angle PBO$，
$\therefore \angle PAO = 2\angle PBO$；

(2)如图 2，连接 $OP$，延长 $BO$ 与 $\odot O$ 交于点 $C$，连接 $PC$，过点 $P$ 作 $PD\perp OC$ 于点 $D$，则有 $AO=\sqrt{AP^{2}+OP^{2}}=\frac{25}{3}$，由
(1)可知 $\angle POC=\angle PAO$，
$\therefore Rt\triangle POD\sim Rt\triangle OAP$，$\therefore \frac{PD}{PO}=\frac{PO}{OA}=\frac{OD}{AP}$，即 $\frac{PD}{5}=\frac{5}{\frac{25}{3}}=\frac{OD}{\frac{20}{3}}$，解得 $PD = 3$，$OD = 4$，$\therefore CD = OC - OD = 1$，
在 $Rt\triangle PDC$ 中，$PC=\sqrt{PD^{2}+CD^{2}}=\sqrt{10}$，$\because CB$ 为 $\odot O$ 的直径，$\therefore \angle BPC = 90^{\circ}$，$\therefore BP=\sqrt{BC^{2}-PC^{2}}=\sqrt{100 - 10}=3\sqrt{10}$，故 $BP$ 的长为 $3\sqrt{10}$。