《2025年考点集训与满分备考九年级数学下册冀教版》

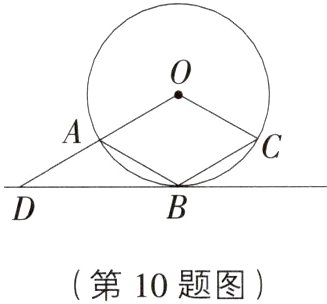
10. 重点 如图，菱形OABC的顶点A，B，C在⊙O上，过点B作⊙O的切线交OA的延长线于点D.若⊙O的半径为1，则BD的长为( )

A. 1
B. √2
C. √3
D. 2

答案： C [解析] 在题图中连接 $OB$，
$\because BD$ 是 $\odot O$ 的切线，$\therefore \angle OBD = 90^{\circ}$，
$\because$ 四边形 $OABC$ 为菱形，$\therefore OA = AB$，
$\because OA = OB$，$\therefore OA = OB = AB$，$\therefore \triangle OAB$ 为等边三角形，$\therefore \angle AOB = 60^{\circ}$，$\therefore \angle ODB = 30^{\circ}$，$\therefore OD = 2OB = 2$，由勾股定理得 $BD=\sqrt{OD^{2}-OB^{2}}=\sqrt{3}$。

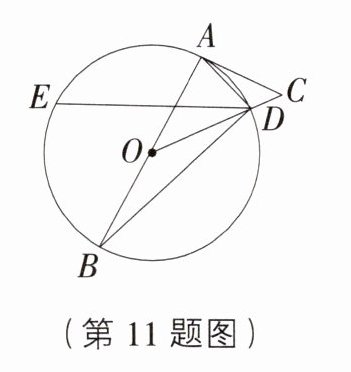
11. 如图，AB为⊙O的直径，直线AC与⊙O相切于点A，点E为半圆⌢AB的中点，连接OC交⊙O于点D，连接ED.若∠CAD=20°，则∠EDO的度数为( )


A. 20°
B. 25°
C. 30°
D. 35°

答案：
B [解析] 如图，连接 $OE$，
$\because$ 直线 $AC$ 与 $\odot O$ 相切于点 $A$，
$\therefore AB\perp AC$，$\therefore \angle BAC = 90^{\circ}$，
$\because \angle BAD = 90^{\circ}-\angle CAD = 90^{\circ}-20^{\circ}=70^{\circ}$，$OA = OD$，$\therefore \angle ODA=\angle OAD = 70^{\circ}$，
$\because$ 点 $E$ 为半圆 $\widehat{AB}$ 的中点，
$\therefore OE\perp AB$，$\therefore \angle AOE = 90^{\circ}$，
$\therefore \angle ADE=\frac{1}{2}\angle AOE = 45^{\circ}$，
$\therefore \angle EDO=\angle ODA-\angle ADE = 70^{\circ}-45^{\circ}=25^{\circ}$。

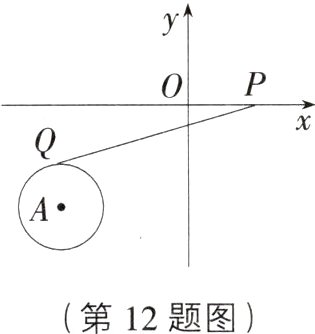
12. 易错题 如图，点A的坐标为(-3,-2)，⊙A的半径为1，P为x轴上一动点，PQ切⊙A于点Q，则当PQ取最小值时，点P的坐标为( )

A. (-4,0)
B. (-2,0)
C. (-4,0)或(-2,0)
D. (-3,0)

答案：
D [解析] 如图，连接 $AQ$，$AP$。根据切线的性质定理，得 $AQ\perp PQ$，
$\therefore PQ=\sqrt{AP^{2}-AQ^{2}}$，$\because AQ = 1$，$\therefore$ 要使 $PQ$ 最小，只需 $AP$ 最小，根据垂线段最短，可知当 $AP\perp x$ 轴时，$AP$ 最短，
$\therefore$ 点 $P$ 的坐标是 $(-3,0)$。

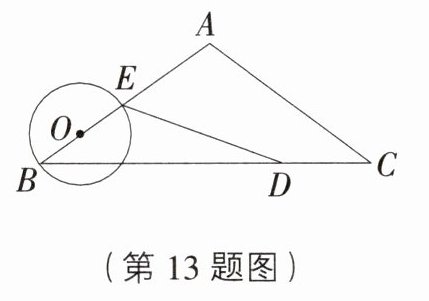
13. 较难题 如图，等腰三角形ABC中，AB=AC=5 cm，BC=8 cm.动点D从点C出发，沿线段CB以2 cm/s的速度向点B运动，同时动点O从点B出发，沿线段BA以1 cm/s的速度向点A运动，当其中一个动点停止运动时另一个动点也随之停止.设运动时间为t(s)，以点O为圆心，OB长为半径的⊙O与BA交于另一点E，连接ED.当直线DE与⊙O相切时，t的取值是( )


A. 16/9
B. 3/2
C. 4/3
D. √3

答案：
A [解析] 如图，过点 $A$ 作 $AH\perp BC$ 于点 $H$，由题可知 $BE = 2t\ cm$，$BD=(8 - 2t)\ cm$，$\because AB = AC = 5\ cm$，$\therefore BH = CH=\frac{1}{2}BC = 4\ cm$，当直线 $DE$ 与 $\odot O$ 相切时，$BE\perp DE$，则 $\angle BED = 90^{\circ}$，
$\because \angle EBD=\angle ABH$，
$\therefore \triangle BED\sim\triangle BHA$，
$\therefore \frac{BE}{BH}=\frac{BD}{BA}$，
即 $\frac{2t}{4}=\frac{8 - 2t}{5}$，解得 $t=\frac{16}{9}$。

14. 应用意识 如图，A，B两地相距a m，它们之间有一半径为r m的圆形绿地(r＜ a/2 )，绿地圆心位于AB连线的中点O处，分别过A，B作⊙O的切线相交于点C，切点分别为点D，E.现规划两条驾车路径：①B→E→C→D→A；②B→E→(沿⌢ED )→D→A，则下列说法正确的是( )

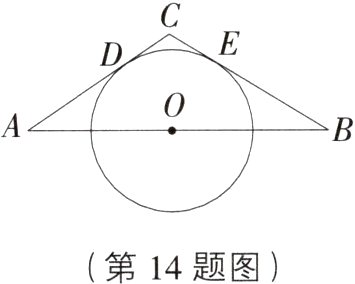
A. ①较长
B. ②较长
C. ①②一样长
D. 以上皆有可能

答案：
A [解析] 如图，①$B\rightarrow E\rightarrow C\rightarrow D\rightarrow A$，所走的路程为 $BE + EC + CD + DA$；②$B\rightarrow E\rightarrow$（沿 $\widehat{ED}$）$\rightarrow D\rightarrow A$，所走的路程为 $BE+\widehat{ED}+DA$；连接 $OC$，$OD$，$OE$，$\because AC$，$BC$ 是 $\odot O$ 的切线，切点分别为 $D$，$E$，$\therefore OD\perp AC$，$OE\perp BC$，$\therefore S_{四边形 ODCE}=\frac{1}{2}CD\cdot OD+\frac{1}{2}CE\cdot OE=\frac{1}{2}(CD + CE)\cdot r$；$S_{扇形 DOE}=\frac{1}{2}\widehat{ED}\cdot r$，
$\therefore S_{四边形 ODCE}＞S_{扇形 DOE}$，$\therefore \frac{1}{2}(CD + CE)\cdot r＞\frac{1}{2}\widehat{ED}\cdot r$，$\therefore EC + CD＞\widehat{ED}$，$\therefore BE + EC + CD + DA＞BE+\widehat{ED}+DA$，即①＞②。

15. 如图，利用垂直于地面的墙面和刻度尺，可以度量出圆的半径为____ cm.

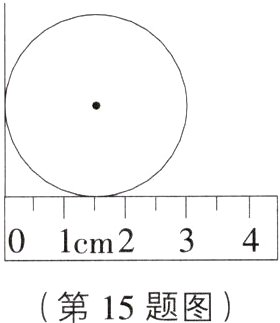
答案：
$1.5$ [解析] 如图，连接 $OD$，$OE$，
$\because \odot O$ 分别与 $AB$，$AC$ 相切，
$\therefore OD$，$OE$ 为 $\odot O$ 的半径，
$\because \angle EAD=\angle ADO=\angle OEA = 90^{\circ}$，而 $OE = OD$，$\therefore$ 四边形 $ODAE$ 为正方形，
$\therefore OE = AD = 1.5\ cm$，
即圆的半径为 $1.5\ cm$。

16. 推理能力 如图，在⊙O中，AB是直径，点D是⊙O上一点，且∠BOD=60°，过点D作⊙O的切线CD交AB延长线于点C，E为⌢AD的中点，连接DE，EB，EB与OD交于点Q.
(1)求证：EB//CD；
(2)已知图中阴影部分面积为6π.
①求⊙O的半径r；
②直接写出图中阴影部分的周长.

答案：
[解析]
(1)如图，连接 $OE$，$\because CD$ 是 $\odot O$ 的切线，$\therefore OD\perp CD$，即 $\angle ODC = 90^{\circ}$，$\because AB$ 是 $\odot O$ 的直径，$\angle BOD = 60^{\circ}$，$E$ 为 $\widehat{AD}$ 的中点，$\therefore \angle EOD=\angle AOE = 60^{\circ}$，$\because OE = OB$，$\therefore OD\perp BE$，$\because OD\perp DC$，$\therefore EB// CD$；

(2)①$\because \angle EOD = 60^{\circ}$，$OE = OD$，
$\therefore \triangle EOD$ 是等边三角形，
$\therefore DE = OD = OB$，$\angle EDQ = 60^{\circ}=\angle BOD$，
在 $\triangle EQD$ 和 $\triangle BQO$ 中，
$\begin{cases}\angle EDQ=\angle BOQ,\\\angle EQD=\angle BQO,\\DE = OB,\end{cases}$
$\therefore \triangle EQD\cong\triangle BQO(AAS)$，
$\therefore S_{\triangle EQD}=S_{\triangle BQO}$，$\therefore$ 阴影部分的面积=扇形 $BOD$ 的面积，$\because$ 图中阴影部分面积为 $6\pi$，$\therefore \frac{60\pi\times OB^{2}}{360}=6\pi$，$\therefore OB = 6$，即 $\odot O$ 的半径是 $6$；
②阴影部分的周长为 $6\sqrt{3}+6 + 2\pi$。
提示：$\because OB = 6$，$\angle BOD = 60^{\circ}$，$\angle OQB = 90^{\circ}$，$\therefore OQ=\frac{1}{2}OB=\frac{1}{2}\times6 = 3$，$\therefore BQ=\sqrt{OB^{2}-OQ^{2}}=\sqrt{6^{2}-3^{2}}=3\sqrt{3}$，
$\because OD\perp BE$，$OD$ 过点 $O$，
$\therefore EQ = BQ = 3\sqrt{3}$，
$\therefore BE = 6\sqrt{3}$，$\widehat{BD}$ 的长是 $\frac{60\pi\times6}{180}=2\pi$，
$\because DE = OB = 6$，$\therefore$ 阴影部分的周长=$BE + DE+\widehat{BD}=6\sqrt{3}+6 + 2\pi$。