《2025年考点集训与满分备考九年级数学下册冀教版》

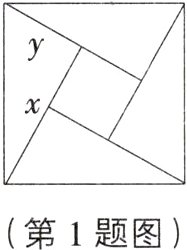
1. 运算能力 如图，是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案（赵爽弦图）.用$x,y$表示直角三角形的两直角边$(x ＞ y)$，并且$(x + y)^2 = 49$，小正方形面积为1.若随机在大正方形及其内部区域投针，则针扎到直角三角形的概率是（ ）

A. $\frac{24}{25}$
B. $\frac{1}{5}$
C. $\frac{3}{4}$
D. $\frac{4}{5}$

答案： A [解析]
∵ 小正方形面积为 1，
∴ 小正方形的边长是 1，
∴ $x - y = 1$，
∴ $(x - y)^2 = 1$，
∴ $x^2 - 2xy + y^2 = 1$ ①，
∵ $(x + y)^2 = 49$，
∴ $x^2 + 2xy + y^2 = 49$ ②，
② - ①得 $4xy = 48$，解得 $xy = 12$，
∴ 四个直角三角形的面积是 $\frac{1}{2}xy×4=\frac{1}{2}×12×4 = 24$，
∴ 针扎到直角三角形的概率是 $\frac{24}{24 + 1}=\frac{24}{25}$。

2. 如图，小华把同心圆纸板挂在墙上玩飞镖游戏（每次飞镖均落在纸板上），已知大圆半径为30 cm，小圆半径为20 cm，则飞镖击中阴影区域的概率是______.

答案： $\frac{5}{9}$ [解析] 大圆面积：$\pi×30^2 = 900\pi$，
小圆面积：$\pi×20^2 = 400\pi$，阴影部分面积：$900\pi - 400\pi = 500\pi$，飞镖击中阴影区域的概率 $P=\frac{500\pi}{900\pi}=\frac{5}{9}$。

3. 如图，正方形的边长为2，中心为$O$，从$O$，$A$，$B$，$C$，$D$五点中任取两点.
（1）求取到的两点间的距离为2的概率；
（2）求取到的两点间的距离为$2\sqrt{2}$的概率；
（3）求取到的两点间的距离为$\sqrt{2}$的概率.

答案： [解析]
(1)从 $O$，$A$，$B$，$C$，$D$ 五点中任取两点，所有等可能出现的结果有 $AB$，$AC$，$AD$，$BC$，$BD$，$CD$，$OA$，$OB$，$OC$，$OD$，共有 10 种，
满足两点间的距离为 2 的结果有 $AB$，$BC$，$CD$，$AD$ 这 4 种，
则 $P(\text{两点间的距离为 }2)=\frac{4}{10}=\frac{2}{5}$；
(2)满足两点间的距离为 $2\sqrt{2}$ 的结果有 $AC$，$BD$ 这 2 种。则 $P(\text{两点间的距离为 }2\sqrt{2})=\frac{2}{10}=\frac{1}{5}$；
(3)满足两点间的距离为 $\sqrt{2}$ 的结果有 $OA$，$OB$，$OC$，$OD$ 这 4 种。则 $P(\text{两点间的距离为 }\sqrt{2})=\frac{4}{10}=\frac{2}{5}$。

4. 游戏公平性 某中学举行演讲比赛.九（1）班的班长和学习委员都想去，于是老师制作了四张标有算式的卡片（除算式外其他都相同），背面朝上洗匀后，先由班长抽一张，再由学习委员在余下三张中抽一张.如果两张卡片上的算式都正确，班长去；如果两张卡片上的算式都错误，学习委员去；如果两张卡片上的算式一个正确一个错误，则都放回去，背面朝上洗匀后再抽.这个游戏公平吗？请用画树形图或列表的方法，结合概率予以说明.

答案：
[解析] 由题意可画树形图如图所示。

∵ 四张卡片中 $B$ 和 $D$ 正确，两张都正确的只有 2 种情况，两张卡片上的算式都错误的只有 $AC$，$CA$ 两种情况，
∴ 班长去的概率为 $\frac{2}{12}=\frac{1}{6}$，
学习委员去的概率为 $\frac{2}{12}=\frac{1}{6}$。故此游戏公平。

5. 在学习“二元一次方程的解”时，数学张老师设计了一个数学活动，有A，B两组卡片，每组各三张，A组卡片上分别写有0，1，2；B组卡片上分别写有-3，-1，1.每张卡片除正面写有不同数字外，其余均相同.甲从A组随机抽取一张记为$x$，乙从B组随机抽取一张记为$y$.
（1）若甲抽出的数字是2，乙抽出的数字是-1，它们恰好是方程$ax - y = 5$的解，求$a$的值；
（2）在（1）的条件下，求甲、乙随机抽取一次的数恰好是方程$ax - y = 3$的解的概率.

答案：
[解析]
(1)将 $x = 2$，$y = - 1$ 代入方程，得 $2a + 1 = 5$，即 $a = 2$；
(2)列表如下。
$ |所有等可能的情况有 9 种，其中 $(x,y)$ 恰好为方程 $2x - y = 3$ 的解的情况有 $(0,-3)$，$(1,-1)$，$(2,1)$，共 3 种情况，则抽取一次的数恰好是方程 $ax - y = 3$ 的解的概率为 $\frac{3}{9}=\frac{1}{3}$。