《2025年考点集训与满分备考九年级数学下册冀教版》

1. 教材P11图29 - 4 - 3衍生 如图，从圆O外一点P引圆O的两条切线PA，PB，切点分别为A，B.如果∠APB = 60°，PA = 8，那么弦AB的长是（ ）

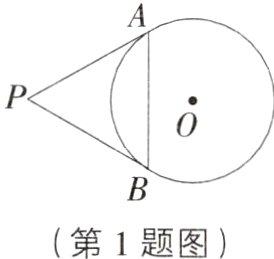
A. 4
B. 8
C. 4√3
D. 8√3

答案： B　[解析]
∵PA,PB都是⊙O的切线，
∴PA = PB，又
∵∠P = 60°，
∴△PAB是等边三角形，即AB = PA = 8.

2. 如图，PA切⊙O于点A，PB切⊙O于点B，OP交⊙O于点C，下列结论中错误的是（ ）

A. ∠APO = ∠BPO
B. PA = PB
C. AB⊥OP
D. C是PO的中点

答案： D　[解析]
∵PA,PB是⊙O的切线，
∴PA = PB，∠BPO = ∠APO，
∴选项A,B不符合题意；
∵PA = PB，∠BPO = ∠APO，
∴OP⊥AB，
∴选项C不符合题意；根据已知条件不能得出C是PO的中点，故选项D符合题意.

3. 教材P14，T3·习题改编 如图，四边形ABCD的四边分别与圆相切，切点分别为E，F，G，H，若四边形ABCD的周长为48，则AB + CD = ______.

答案： 24[解析]
∵四边形ABCD的四边分别与圆相切，
∴AE = AH，BE = BF，CF = CG，DH = DG，
∴AD + BC = AB + CD.
∵四边形ABCD的周长 = AD + BC + AB + CD = 48，
∴AB + CD = 24.

4. 如图，直线AB，BC，CD分别与⊙O相切于E，F，G，且AB//CD，OB = 6 cm，OC = 8 cm.求：
（1）∠BOC的度数；
（2）BE + CG的长；
（3）⊙O的半径.

答案： [解析]
(1)在题图中连接OF，根据切线长定理得BE = BF，CF = CG，∠OBF = ∠OBE，∠OCF = ∠OCG.
∵AB//CD，
∴∠ABC + ∠BCD = 180°，
∴∠OBF + ∠OCF = 90°，
∴∠BOC = 90°.
(2)由
(1)知，∠BOC = 90°.
∵OB = 6cm，OC = 8cm，由勾股定理得BC = √(OB² + OC²) = 10cm，
∴BE + CG = BF + CF = BC = 10cm.
(3)由题意得OF⊥BC，
∴S△OBC = 1/2×OF×BC = 1/2×OB×OC，即1/2×OF×10 = 1/2×6×8，
∴OF = 4.8cm.
∴⊙O的半径为4.8cm.

5. 如图，△ABC中，AB = AC，∠ABC = 70°，点O是△ABC的内心，则∠BOC的度数为（ ）

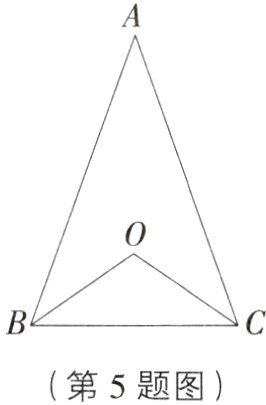
A. 120°
B. 110°
C. 115°
D. 130°

答案： B　[解析]
∵AB = AC，
∴∠ACB = ∠ABC = 70°，
∵点O是△ABC的内心，
∴∠OBC = 1/2∠ABC = 35°，∠OCB = 1/2∠ACB = 35°，
∴∠OBC + ∠OCB = 70°，
∴∠BOC = 180° - (∠OBC + ∠OCB) = 110°.

6. 教材P14，AT2·习题变式 已知△ABC的内切圆半径r = √3，D，E，F为切点，∠ABC = 60°，BC = 8，S△ABC = 10√3，求AB，AC的长.

答案：
[解析]如图，连接OA,OB,OC,OE,OF,OD，
∵△ABC的内切圆半径r = √3，D,E,F为切点，∠ABC = 60°，
∴∠ABO = ∠CBO = 30°，
∴BE = BD = √3OE = 3，
∵BC = 8，
∴CD = 8 - 3 = 5 = CF，
∵S△ABC = 10√3，
∴1/2×(AB + BC + AC)×r = 10√3，
∴1/2×(AE + 3 + 8 + 5 + AF)×√3 = 10√3，
∴AE = AF = 2，即AC = 5 + 2 = 7，AB = 3 + 2 = 5.

7. 如图，在△ABC中，∠BOC = 140°，I是内心，O是外心，则∠BIC等于（ ）

A. 130°
B. 125°
C. 120°
D. 115°

答案： B　[解析]
∵在△ABC中，∠BOC = 140°，O是外心，
∴∠BOC = 2∠A，
∴∠A = 70°，
∴∠ABC + ∠ACB = 180° - ∠A = 110°，
∵I为△ABC的内心，
∴∠IBC = 1/2∠ABC，∠ICB = 1/2∠ACB，
∴∠IBC + ∠ICB = 1/2×110° = 55°，
∴∠BIC = 180° - (∠IBC + ∠ICB) = 125°.