《2025年考点集训与满分备考九年级数学下册冀教版》

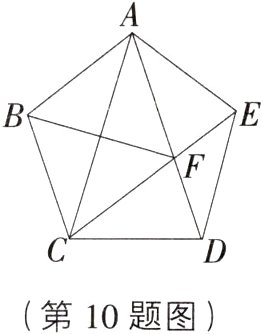
10. 如图，在正五边形ABCDE中，连接AC，AD，CE，CE交AD于点F，连接BF，下列说法不正确的是 ( )

A. △CDF的周长等于AD + CD
B. FC平分∠BFD
C. $AC^{2}+BF^{2}=4CD^{2}$
D. 四边形ABCF是菱形

答案： B [解析]
∵五边形 ABCDE 是正五边形，
∴AB = BC = CD = DE = AE，BA//CE，AD//BC，AC//DE，AC = AD = CE.
∴四边形 ABCF 是菱形，故 D 说法正确.
∴CF = AF，
∴△CDF 的周长等于 CF + DF + CD = AF + DF + CD = AD + CD，即△CDF 的周长等于 AD + CD，故 A 说法正确.
∵四边形 ABCF 是菱形，
∴AC⊥BF，设 AC 与 BF 交于点 O，由勾股定理，得 OB² + OC² = BC²，
∴AC² + BF² = (2OC)² + (2OB)² = 4OC² + 4OB² = 4BC²，
∵BC = CD，
∴AC² + BF² = 4CD²，故 C 说法正确.无法通过已知条件证明 FC 平分∠BFD，故 B 错误.

11. 创新设问 如图，有公共顶点O的两个边长为3的正五边形(不重叠)，以点O为圆心，半径为3作圆，构成一个“蘑菇”形图案，则这个“蘑菇”形图案(阴影部分)的面积为 ( )

A. 4π
B. $\frac{18}{5}\pi$
C. 3π
D. $\frac{5}{2}\pi$

答案： B
[解析] $S_{阴}=\frac{(360 - 108×2)·\pi·3^{2}}{360}=\frac{18}{5}\pi$.

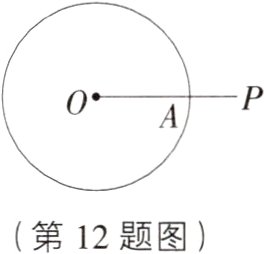
12. 如图，已知P为⊙O外一点，连接OP交⊙O于点A，且OA = 2AP，求作直线PB，使PB与⊙O相切. 以下是甲、乙两同学的作业.
甲：作OP的中垂线，交⊙O于点B，则直线PB即为所求.
乙：取OP的中点M，以M为圆心，OM长为半径画弧，交⊙O于点B，则直线PB即为所求.
对于两人的作业，下列说法正确的是( )

A. 两人都对
B. 两人都不对
C. 甲对，乙不对
D. 甲不对，乙对

答案：
D [解析] 如图 1，OP 的垂直平分线交 OP 于 H，连接 OB，设 AP = x，则 OA = 2x，OB = 2x，
∵BH 垂直平分 OP，
∴BO = BP = 2x，
∵OB² + BP² = (2x)² + (2x)² = 8x²，OP² = (3x)² = 9x²，
∴△OBP 不是直角三角形，
∴PB 不是⊙O 的切线，所以甲的作法错误；如图 2，连接 OB，
∵点 M 为 OP 的中点，
∴OP 为⊙M 的直径，
∴∠OBP = 90°，
∴OB⊥PB，
∴PB 与⊙O 相切，所以乙的作法正确.

13. 若一个正多边形的中心角为40°，则这个正多边形的内角和是______°.

答案： 1 260 [解析]
∵正多边形的一个中心角为 40°，
∴360°÷40° = 9，
∴这个正多边形是正九边形，
∴这个正九边形的内角和等于(9 - 2)×180° = 1 260°.

14. 如图，正方形ABCD的边长为4，⊙O的半径为1. 若⊙O在正方形ABCD内平移(⊙O可以与该正方形的边相切)，则点A到⊙O上的点的距离的最大值为______.

答案：
$3\sqrt{2}+1$ [解析] 如图，当⊙O 与 CB，CD 相切时，点 A 到⊙O 上的点 Q 的距离最大，连接 AC，OE，OF，
∵OE⊥BC，OF⊥CD，OE = OF = 1，
∴CO 平分∠BCD，
∵四边形 ABCD 为正方形，
∴点 O 在 AC 上，
∵AC=$\sqrt{2}$BC = 4$\sqrt{2}$，OC=$\sqrt{2}$OE=$\sqrt{2}$，
∴AO = AC - OC = 3$\sqrt{2}$，
∴AQ = OA + OQ = 3$\sqrt{2}+1$，
即点 A 到⊙O 上的点的距离的最大值为 3$\sqrt{2}+1$.

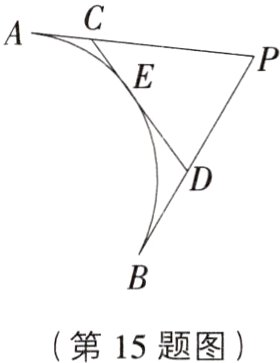
15. 如图，PA，PB，CD分别与同一段圆弧$\overset{\frown}{AB}$相切于点A，B，E，若∠P = 60°，△PCD的周长为$4\sqrt{3}$，则$\overset{\frown}{AB}$的长度为______.

答案：
$\frac{4}{3}\pi$ [解析] 如图，设圆弧$\overset{\frown}{AB}$的圆心为 O，连接 OA，OB，
∵PA，PB 都是圆 O 的切线，
∴PA = PB，∠OAP = ∠OBP = 90°，
同理 AC = CE，DE = DB，
∴△PCD 的周长 = PC + CD + PD = PC + CE + DE + PD = PC + CA + DB + PD = PA + PB = 4$\sqrt{3}$，
∴PA = 2$\sqrt{3}$；连接 PO，
∵∠APB = 60°，
∴∠APO = 30°，∠AOP = 60°，
∴∠AOB = 120°，
AO = AP×tan∠APO = 2$\sqrt{3}$×$\frac{\sqrt{3}}{3}$= 2，
∴$\overset{\frown}{AB}=\frac{120×\pi×2}{180}=\frac{4}{3}\pi$.

16. 如图，△ABC中，AC = 8，∠A = 30°，∠B = 50°，点P为AB边上任意一点(P不与点B，C重合)，I为△BPC的内心，则：
(1)CP的最小值=______；
(2)∠CIB的取值范围是____________.

答案：
(1)4
(2)105°＜∠BIC＜155°
[解析]
(1)根据垂线段最短可知：当 CP⊥AB 时，PC 的值最小，
此时∠APC = 90°，∠A = 30°，
∴PC=$\frac{1}{2}$AC = 4；
(2)
∵I 为△BPC 的内心，
∴∠IBC=$\frac{1}{2}$∠PBC，∠ICB=$\frac{1}{2}$∠PCB，
∴∠BIC = 180° - (∠IBC + ∠ICB)=180°-$\frac{1}{2}$(∠PBC + ∠PCB)=180°-$\frac{1}{2}$(180° - ∠BPC)=90°+$\frac{1}{2}$∠BPC，
∵30°＜∠BPC＜130°，
∴105°＜∠BIC＜155°.

17. (6分)如图，在△ABC中，AB = AC，D为BC的中点，DE⊥AB于点E，以点D为圆心、DE为半径作⊙D，试判断⊙D与直线AC的位置关系，并给予证明.

答案：
[解析] ⊙D 与直线 AC 相切.
理由：如图，连接 AD，过 D 作 DF⊥AC 于 F.
∵AB = AC，D 为 BC 的中点，
∴∠BAD = ∠CAD.
∵DE⊥AB，DF⊥AC，
∴DF = DE，即圆心 D 到直线 AC 的距离等于半径，
∴⊙D 与直线 AC 相切.